Охлаждения формула – Количество теплоты: нагревание, охлаждение, плавление, кристаллизация, парообразование, конденсация, горение. Термодинамическая система
Количество теплоты: нагревание, охлаждение, плавление, кристаллизация, парообразование, конденсация, горение. Термодинамическая система
Тестирование онлайн
Количество теплоты. Основные понятия
Количество теплоты
Термодинамика
Раздел молекулярной физики, который изучает передачу энергии, закономерности превращения одних видов энергии в другие. В отличие от молекулярно-кинетической теории, в термодинамике не учитывается внутреннее строение веществ и микропараметры.
Термодинамическая система
Это совокупность тел, которые обмениваются энергией (в форме работы или теплоты) друг с другом или с окружающей средой. Например, вода в чайнике остывает, происходит обмен теплотой воды с чайником и чайника с окружающей средой. Цилиндр с газом под поршнем: поршень выполняет работу, в результате чего, газ получает энергию, и изменяются его макропараметры.
Количество теплоты
Это энергия, которую получает или отдает система в процессе теплообмена. Обозначается символом Q, измеряется, как любая энергия, в Джоулях.
В результате различных процессов теплообмена энергия, которая передается, определяется по-своему.
Нагревание и охлаждение
Этот процесс характеризуется изменением температуры системы. Количество теплоты определяется по формуле
Удельная теплоемкость вещества с измеряется количеством теплоты, которое необходимо для нагревания единицы массы данного вещества на 1К. Для нагревания 1кг стекла или 1кг воды требуется различное количество энергии. Удельная теплоемкость – известная, уже вычисленная для всех веществ величина, значение смотреть в физических таблицах.
Теплоемкость вещества С – это количество теплоты, которое необходимо для нагревания тела без учета его массы на 1К.
Плавление и кристаллизация
Плавление – переход вещества из твердого состояния в жидкое. Обратный переход называется кристаллизацией.
Энергия, которая тратится на разрушение кристаллической решетки вещества, определяется по формуле
Удельная теплота плавления известная для каждого вещества величина, значение смотреть в физических таблицах.
Парообразование (испарение или кипение) и конденсация
Парообразование – это переход вещества из жидкого (твердого) состояния в газообразное. Обратный процесс называется конденсацией.
Удельная теплота парообразования известная для каждого вещества величина, значение смотреть в физических таблицах.
Горение
Количество теплоты, которое выделяется при сгорании вещества
Удельная теплота сгорания известная для каждого вещества величина, значение смотреть в физических таблицах.
Для замкнутой и адиабатически изолированной системы тел выполняется уравнение теплового баланса. Алгебраическая сумма количеств теплоты, отданных и полученных всеми телами, участвующим в теплообмене, равна нулю:
Q1+Q2+…+Qn=0
fizmat.by
Нагревание и охлаждение тел – Класс!ная физика
Нагревание и охлаждение тел
При нагревании тело получает тепло, а при охлаждении отдает его.
Количество теплоты, полученное телом при нагревании, можно рассчитать по формуле:
где с – удельная теплоемкость вещества,
m – масса вещества,
– разность конечной и начальной температур.
Эта же формула годится для расчета количества теплоты, выделившейся при охлаждении тела.
Удельная теплоемкость вещества – это физическая величина, показывающая количество теплоты, которое нужно передать 1 кг этого вещества для нагревания его на 1 °С.
Единица измерения удельной теплоемкости в системе СИ:
[ с ] = 1 Дж/(кг°С).
При охлаждении тела до прежней температуры выделяется такое же количество теплоты, которое было затрачено на нагревание этого тела.
…………………..
ИНТЕРЕСНО
1. Почему в водоемах летом вода на достаточной глубине плохо прогревается?
Нагревание воды солнечными лучами происходит сверху. Однако вода обладает плохой теплопроводностью.
2. Почему зимой на глубине у дна водоема сохраняется температура +4 градуса по Цельсию?
Первое – лёд не тонет.
Второе – вода, охладившаяся до +4 градусов по Цельсию, обладает наибольшей плотностью, поэтому опускается на дно.
Третье – плохая теплопроводность воды не может привести к выравниванию температуры по всей глубине.
Нагревание пузырька плотничьего уровня.
С помощью этого прибора плотники выставляют горизонтальный уровень при строительных работах.
Если прибор лежит на горизонтальной поверхности, то пузырек воздуха, имеющийся в стеклянной трубке, заполненной водой, будет располагаться ровно по центру. При наклоне уровня пузырек сместится к одному из концов трубки.
Длина пузырька воздуха меняется при колебаниях температуры. Но, как? Когда пузырек больше: в теплую или в холодную погоду? В этих условиях газ не может расширяться, т.к. этому препятствует замкнутая в уровне жидкость. При нагревании расширение жидкости окажется больше расширения трубки, что и сжимает пузырек.
А, ты, согласен с этим ?
___
Очень часто лед используется для охлаждения. Это возможно, потому что при таянии (плавлении) льда поглощается большое количество тепла.
class-fizika.ru
Нагревание и охлаждение идеального однородного твердого тела
Дата публикации: .
Уравнение нагревания
Хотя электрическая машина имеет сложное устройство, в основу анализа процесса ее нагревания может быть положена теория нагревания идеального однородного твердого тела, под которым здесь понимается тело, обладающее равномерным рассеянием тепла со всей поверхности и бесконечно большой теплопроводностью, вследствие чего все точки тела имеют одинаковую температуру. Составим дифференциальное уравнение нагревания такого тела, для чего рассмотрим его тепловой баланс.
Пусть в единицу времени в теле выделяется количество теплоты Q. Тогда за бесконечно малый промежуток времени выделяемое количество теплоты будет равно Q × dt. Эта теплота частично аккумулируется в теле при повышении температуры и частично отдается во внешнюю среду.
Если за время dt температура тела повысилась на dΘ, то количество аккумулируемой за это время теплоты равно G × c × dΘ, где G – масса тела и c – его удельная теплоемкость.
Пусть в рассматриваемом бесконечно малом интервале времени превышение температуры тела над температурой окружающей среды равно Θ. Тогда количество теплоты, отдаваемое в окружающее пространство за время dt вследствие лучеиспускания, конвекции и теплопроводности, будет равно S × λ × Θ × dt, где S – площадь тела и λ – коэффициент теплоотдачи с поверхности.
На основе закона сохранения энергии
| Q × dt = G × c × dΘ + S × λ × Θ × dt . | (1) |
Прежде чем приступить к решению уравнения нагревания (1), несколько преобразуем его.
Установившееся превышение температуры и постоянная времени нагревания
После истечения достаточно длительного времени (теоретически при t = ∞) температура тела достигает установившегося значения. Тогда dΘ = 0 и Θ = Θ∞. Подставив эти значения в выражение (1), получим
Q ×dt = S × λ × Θ∞ × dt ,
откуда
| (2) |
Установившееся превышение температуры Θ∞ тем больше, чем больше выделяется тепла и чем хуже условия ее отдачи, то есть чем меньше S × λ.
Разделим обе части выражения (1) на S × λ, используем равенство (2) и обозначим
| (3) |
Тогда вместо (1) получим
| Θ∞ × dt = T × dΘ + Θ × dt. | (4) |
Размерность всех членов (4) должна быть одинакова – температура, умноженная на время. Поэтому T имеет разность времени, что можно установить также по формуле (3). Величина T называется постоянной времени нагревания тела; согласно формуле (3), она тем больше, чем больше теплоемкость тела G × c и чем меньше интенсивность отдачи тепла, то есть меньше S × λ.
Если определить из равенства (2) S × λ и подставить в (3), то получим еще одно выражение для T:
| (5) |
Числитель этого выражения равен количеству теплоты, накопленной в теле при достижении Θ = Θ∞.
Следовательно, в соответствии с выражением (5) постоянная времени нагревания T равна времени, в течение которого температура достигла бы установившегося значения Θ∞, если бы отсутствовала передача тепла в окружающую среду и все выделяемое тепло накапливалось в теле.
Решение уравнения нагревания
В уравнении (4) можно разделить переменные и привести его к виду
| (6) |
При интегрировании уравнения (6) получим
| t / T = – ln (Θ∞ – Θ) + C . | (7) |
Постоянная C определяется из начального условия: при t = 0 тело в общем случае имеет некоторое превышение температуры Θ = Θ0. Подставив указанные значения t и Θ в (7), найдем, что
C = ln (Θ∞ – Θ0) .
Подставим это значение C в (7) и переменим знаки. Тогда
откуда окончательно для Θ = f(t) находим
| Θ = Θ∞ × (1 – e–t/T) + Θ0 × e–t/T . | (8) |
Случай нагревания при Θ0 = 0
В этом случае вместо выражения (8) имеем
| (9) |
чему соответствует экспоненциальная кривая нагревания, изображенная на рисунке 1, а. При малых t, когда и Θ мало, теплопередача в окружающее пространство также мала, большая часть тепла накапливается в теле и температура его растет быстро, как это видно из рисунка 1, а. Затем с ростом Θ теплоотдача увеличивается и рост температуры тела замедляется. При t = ∞, согласно равенству (9), Θ = Θ∞.
На рисунке 1, а указаны значения Θ, достигаемые через интервалы времени T, 2T, 3T и 4T. Из этого рисунка видно, что тело достигает практически установившегося превышения температуры через интервал времени t = 4T.
Охлаждение тела
Если тело имеет некоторое начальное превышение температуры Θ ≠ 0, но Q = 0 и, следовательно, в соответствии с выражением (2) Θ∞ = 0, то происходит охлаждение тела от Θ = Θ0 до Θ = Θ∞ = 0.
Подставив в (8) Θ∞ = 0, получим уравнение охлаждения тела
Экспоненциальная кривая охлаждения тела согласно уравнению (10) представлена на рисунке 1, б. Сначала, когда Θ и соответственно также теплоотдача велики, охлаждение идет быстро, а по мере уменьшения Θ охлаждение замедляется. При t = ∞ будет Θ = 0.
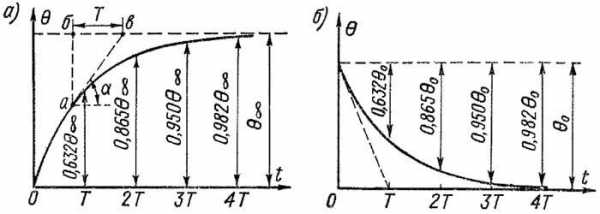
Рисунок 1. Кривые нагревания (а) и охлаждения (б) идеального однородного твердого тела
Общий случай нагревания тела
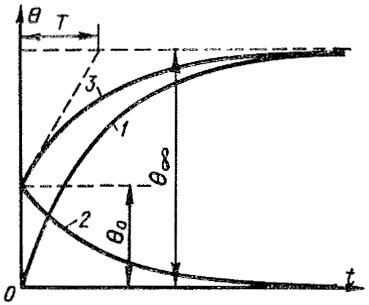 |
| Рисунок 2. Общий случай нагревания идеального однородного твердого тела |
Общий случай нагревания тела, описываемый уравнением (8), на основании формул (9) и (10) можно рассматривать как наложение двух режимов: 1) нагревания тела от начального превышения температуры Θ = 0 до Θ = Θ∞ и 2) охлаждения тела от Θ = Θ0 до Θ = 0. На рисунке 2 кривая 3 представляет собой кривую нагревания, построенную по уравнению (8). Эту кривую можно получить путем сложения ординат кривых 1 и 2, соответствующих уравнениям (9) и (10).
Графический способ определения T
Найдем подкасательную бв (рисунок 1, а), отсекаемую на асимптоте Θ = Θ∞ касательной к кривой Θ = f (t). Из рисунка 1, а следует, что
| (11) |
где α – угол наклона касательной к кривой Θ = f(t).
Как известно,
Но, согласно выражению (6),
| (12) |
Подставив tg α из (12) в (11), получим
бв = T .
Таким образом, подкасательная к любой точке кривой нагревания или охлаждения равна постоянной времени нагревания T. Этим свойством кривых Θ = f(t) можно воспользоваться для графического определения T, если имеется кривая Θ = f(t), снятая, например, опытным путем. На рисунке 1, б и 2 показан способ определения T при построении касательной к начальной кривой.
Заключительные замечания
Выше была изложена теория нагревания идеального однородного твердого тела. В действительности электрическая машина не представляет собой такого тела, так как она состоит из разных частей, обладающих конечной теплопроводностью, причем теплопроводность электрической изоляции достаточно мала. Поэтому отдельные части машины (обмотка, сердечники и другие) имеют различные температуры. В связи с этим более правильно было бы рассматривать электрическую машину как совокупность нескольких однородных тел, между которыми существует теплообмен. В действительных условиях величина T также не вполне постоянна, так как коэффициенты теплоотдачи зависят в определенной мере от температуры. Кроме того, воздух или другой охлаждающий агент при протекании по вентиляционным каналам нагревается, и поэтому температура охлаждающей среды для различных участков охлаждаемой поверхности имеет различные значения.
Таким образом, кривые нагревания и охлаждения не являются, строго говоря, экспоненциальными. Однако в большинстве практических случаев мы не делаем существенных ошибок, считая их экспоненциальными, то есть применяя изложенную выше теорию нагревания идеального однородного тела.
Источник: Вольдек А. И., “Электрические машины. Учебник для технических учебных заведений” – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
www.electromechanics.ru
Формула охлаждения для чиллера
- Подробности
Современный рынок промышленного оборудования предлагает холодильные установки разных моделей. Чтобы эффективно решить поставленные задачи охлаждения, необходимо сделать правильный выбор чиллера, опираясь на требуемые технические параметры и технологический процесс. Однако следует учитывать и интенсивность работы чиллера. Так, если оборудованию предстоит работать в широком диапазоне температур, лучше предусмотреть не одно, а несколько, менее мощных холодильных устройств. Ведь в противном случае между сменами режимов работы чиллер будет работать при неполной загрузке, потребляя при этом большое количество электроэнергии, а постоянное включение и отключение его может привести к выходу из строя отдельных узлов.
Для подбора холодильного оборудования используется формула охлаждения, которая определяет количество холода, которое требуется для охлаждаемой системы и количество холода, которое может произвести чиллер. Формула охлаждения для воды выглядит так:
Q(кВт) = G (л/час) x (Тн – Тk)/1000 x 1,163 или
Q (кКал) = G (л/час) x (Тн – Тk)/1000 или
Q(кВт) = G (м3/час) x (Тн – Тk) x 1,163 ,
в зависимости от того, в каких величинах вести расчёт. Формула для жидкостей в целом:
Q (кВт) = G x (Тнж– Тkж) x Cpж x rж / 3600, где
G (м3/час) – это объём расходуемой жидкости, которую требуется охладить;
Тk (°С) – температура охлаждаемой жидкости, которой следует добиться;
Тн(°С) – температура жидкости на входе.
Cpж ( кДж/(кг °С)) – удельная теплоёмкость жидкости, подвергаемой охлаждению, представляет собой табличное значение.
Rж ( кг/м3)– плотность данной жидкости, также берётся из таблицы.
Процесс подбора холодильной установки лучше доверить опытным специалистам, которые смогут грамотно произвести расчёты и учесть другие технические моменты, например, расположение чиллера относительно охлаждаемого объекта. К примеру, если охлаждающая установка будет находиться на некотором удалении от станка или ванны, то с увеличение длины теплообменника увеличиваются и его теплопотери.
Квалифицированные сотрудники компании Питер Холод готовы произвести расчёт всей охлаждающей системы, выполнить подбор чиллера, произвести подготовительные и монтажные работы на объекте, обслужить или отремонтировать оборудование. Богатый опыт и чёткая специализация позволяют нам реализовывать услуги на высоком профессиональном уровне.
piterholod.ru
Формула количества теплоты
Здесь – количество теплоты, – удельная теплоёмкость вещества, из которого состоит тело, – масса тела, – разность температур.
Единица измерения количества теплоты — Дж (Джоуль) или кал (калория).
По сути тепловая энергия – это внутренняя энергия тела, значит потеря тепла – это уменьшение внутренней энергии тела, а нагревание – увеличение. Удельная теплоёмкость – это характеристика вещества, обозначающая его способность накапливать в себе внутреннюю (тепловую) энергию. Чем она меньше, тем легче вещество нагреть или охладить. Она не пропорциональна плотности, то есть более плотное вещество не обязательно будет нагреваться легче, чем менее плотное. Одно из веществ с большой теплоёмкостью – вода ( Дж/(кг * К)).
Примеры решения задач по теме «Количество теплоты»
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Воздушное охлаждение.
Поскольку коэффициент теплоотдачи от нагретых деталей двигателя в воздух примерно в 10-20 раз меньше, чем при жидкостном охлаждении, то для обеспечения требуемого теплорассеивания при воздушном охлаждении приходится применять оребрение цилиндров и их головок. Наличие ребер в 15-20 раз увеличивает наружную поверхность охлаждаемых деталей и позволяет обеспечить поддержание нормального теплового состояния двигателя.
Ребра на поверхности цилиндра и головки образуются при их отливке или могут быть получены путем механической обработки. Форма, число и расположение ребер обусловлены распределением и интенсивностью тепловых потоков через детали и оказывают весьма существенное влияние на их тепловое состояние.
Наибольшую площадь оребрения обычно имеют головки цилиндров, через которые отводится до 50-70% теплоты.
На современных двигателях воздушного охлаждения чаще всего используются трапециевидные ребра (рис. 6 б), которые более удобны в производстве и в то же время имеют высокую тепловую эффективность. Толщина ребер обычно составляет 2—4 мм, а длина колеблется от 50—70 мм в головке до 20—30 мм на поверхности цилиндра. Дальнейшее увеличение длины ребер не дает существенного повышения их теплорассеивающей способности, так как вследствие роста термического сопротивления теплоотдача от наиболее удаленных участков уменьшается.
Рис. 6 Конструкция охлаждающих ребер:
а – прямоугольное; б – трапециевидное; в – треугольное.
Тепловая эффективность оребрения зависит от шага ребер. При уменьшении шага увеличивается гидравлическое сопротивление движению воздуха и в случае недостаточного напора уменьшается его циркуляция в межреберном канале. Увеличение шага ребер уменьшает гидравлические сопротивления, но зато сокращает их число и общую теплорассеивающую поверхность. Оптимальным можно считать расстояние между ребрами 4-8 мм
Для обеспечения надежного охлаждения необходимо, чтобы скорость движения воздуха в межреберном канале составляла 25- 40 м/сек. В этом случае обеспечивается необходимая турбулизация воздуха, уменьшается ламинарный пограничный слой на поверхности ребер и увеличивается коэффициент теплоотдачи.
Для снижения затрат мощности на привод вентилятора конструкция оребрения должна обеспечить наилучшее использование охлаждающего воздуха, т. е. его максимальный нагрев в межреберном канале. Последнее помимо целесообразной конструкции оребрения достигается рациональной организацией циркуляции воздуха в системе, что обеспечивается применением экранов, отражателей, направляющих ребер и рефлекторов. Кроме выполнения этой функции указанные элементы играют большую роль в обеспечении требуемой равномерности охлаждения различных участков оребрения.
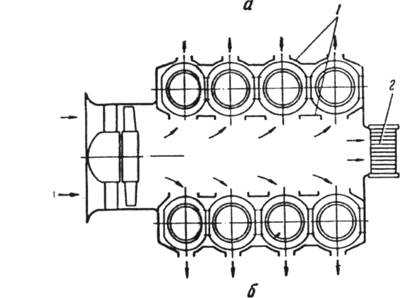
На рис. 7 показаны схемы организации циркуляции воздуха в двигателях воздушного охлаждения.
Как можно видеть из рисунка наличие дефлекторов вокруг каждого цилиндра уменьшает сечение для входа воздуха в систему оребрения. За счет этого ограничивается количество воздуха, входящее в межреберные каналы каждого цилиндра, и предотвращается его повышенный расход. Кроме того, дефлекторы не позволяют воздуху свободно выходить из межреберного канала и увеличивают путь, на котором совершается теплоотдача.
Наличие дефлекторов улучшает также охлаждение тыльной стороны цилиндра, которая находится в наиболее неблагоприятных условиях.
Поскольку нормальное воздушное охлаждение требует высоких скоростей воздуха, то для обеспечения его циркуляции применяются только высокоэффективные осевые вентиляторы с большим числом профилированных лопаток. Полный напор таких вентиляторов составляет 100-240 мм вод. ст. и обеспечивается за счёт относительно высоких окружных скоростей вращения крыльчаток.
Вентиляторы двигателей с воздушным охлаждением, как правило, имеют неподвижный кожух и иногда выполняются с направляющим и спрямляющим аппаратами. В некоторых конструкциях применяются центробежные вентиляторы.
В зависимости от компоновочных условий вентиляторы могут устанавливаться для работы на нагнетание или отсасывание воздуха. В последнем случае объёмная производительность вентилятора, через который проходит горячий воздух, должна быть увеличена, что при разных аэродинамических сопротивлениях воздушного тракта приводит к повышенной затрате мощности.
 |
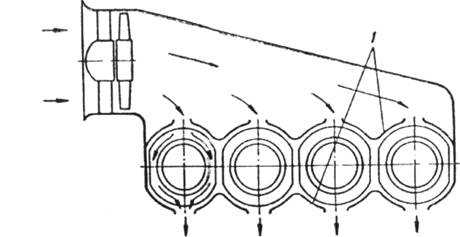 |
| Рис. 7. Схемы организации циркуляции воздуха в двигателях воздушного охлаждения: а – однорядного; б – двухрядного; 1 – дефлектор; 2 – масляный радиатор. |
4. Расчёт системы охлаждения.
Система охлаждения обычно рассчитывается для номинального режима работы двигателя, причём температура окружающей среды принимается равной 40. Системы охлаждения машин, специально предназначены для эксплуатации в тропическом климате, рассчитываются при . Температура жидкости на выходе из двигателя принимается 90-95 °С.
Расчётное количество теплоты которое должно отводится системой охлаждения, определяется по формуле:
где – относительное количество теплоты, отводимое системой охлаждения;
– удельный расход топлива на номинальном режиме, ;
– номинальная мощность двигателя;
– низшая теплота сгорания топлива.
Относительное количество теплоты , отводимое системой охлаждения, можно найти по данным теплового баланса для подобного двигателя или принять по ориентировочным статистическим данным в пределах: 0.20-0.30 – для карбюраторных двигателей, 0.18-0.25 – для дизелей.
где – коэффициент теплопередачи радиатора
– площадь теплорассеивающей поверхности радиатора,
, – средняя температура жидкости и воздуха соответственно,
Требуемая поверхность охлаждения радиатора определяется из уравнения теплопередачи:
Величину коэффициента теплопередачи находят по данным тепловых исследований решеток радиатора.
Перепад средних температур при первоначальном определении можно принимать в пределах
Площадь лобовой поверхности радиатора может быть найдена по формуле:
где – коэффициент компактности сердцевины радиатора, равный 600-950 1/м;
– глубина радиатора, м.
Глубину радиатора определяют с учетом указанных выше рекомендаций относительно числа рядов трубок и выбранного их типоразмера. Обычно глубина радиаторов автомобильного типа составляет 40-80 мм, а глубина решеток сердцевины тяжелых колесных и гусеничных машин — 80- 130 мм.
Учитывая требования компоновки радиатора в моторном отсеке, принимают относительную высоту радиатора и определяют размеры его сердцевины:
Высоту:
Ширину:
По найденным размерам сердцевины вычисляется общее число трубок радиатора:
где – шаг трубок по фронту, м
– число рядов трубок.
Расход воздуха через радиатор:
Температура воздуха на выходе из радиатора:
где – температура на входе в радиаторе, ; ;
– средняя теплоемкость воздуха при постоянном давление.
Требуемый расход охлаждающей жидкости находят по уравнению:
где – площадь поперечного сечения трубки радиатора, ;
– скорость жидкости в трубках радиатора, равная 0.7-1 м/с;
– удельный вес жидкости,
Температура жидкости на выходе из радиатора определяется по формуле:
где – температура жидкости на входе в радиаторе, равная 90-95 ;
– ;
Зная температуру воздуха и жидкости, можно определить действительный средний температурный перепад:
В заключение расчета целесообразно проверить действительную теплорассеивающую способность радиатора:
Если , найденного по формуле (4.17), необходимо скорректировать ранее принятое значение температурного перепада и повторить расчет поверхности радиатора.
Вместимость системы охлаждения можно найти исходя из условий 4-12-кратной циркуляции в жидкостном контуре, а также по эмпирической удельной емкости:
-для легковых автомобилей:
-для грузовых автомобилей:
Расчет жидкостного насоса при учебном проектировании может быть ограничен выбором его размеров, определением скорости вращения и потребляемой мощности.
Окружная скорость на внешнем диаметре крыльчатки насоса определяется по формуле:
где , – углы между направлениями скоростей жидкости на выходе из колеса и окружной скорости;
– расчетный напор насоса, равный 5-15 м вод.ст;
– гидравлический к.п.д. насоса;
Приняв на основании статистических данных наружный диаметр крыльчатки , число ее оборотов можно найти из соотношения:
Мощность, потребляемая насосом:
где – коэффициент подачи насоса;
– общий к.п.д. насоса, обычно равный 0.45-0.6.
Исходными данными для расчета вентилятора являются его производительность и полный набор напор:
(4.32)
где – аэродинамическое сопротивление радиатора(205…600 Н/м2)
– аэродинамическое сопротивление моторного отсека, которое можно принимать равным .
Секундная производительность вентилятора:
где – расход воздуха, кг/ч;
– удельный вес воздуха, кг/м3 ;
Потребная окружная скорость на периферии лопаток рабочего колеса может быть найдена из уравнения:
где
– безразмерная коэффициент напора вентилятора. Коэффициент напора автомобильных вентиляторов составляет:
-для штампованных лопастей
-для литых профилированных лопастей
Наружный диаметр вентилятора лучше всего принимать равным наименьшему размеру лобовой поверхности радиатора или или близким к нему.
Необходимое число оборотов вентилятора:
Диаметр втулки вентилятора можно найти из соотношения:
где – относительная осевая скорость воздуха в вентиляторе, обычно равная 0.2-0.3 для штампованных и 0.30-0.45 для литых профилированных лопастей.
Угол наклона лопастей обычно принимается равным 30-400 , а ширина лопасти – 50-80 мм.
Мощность, потребная вентилятором на расчетном режиме:
где – к.п.д. вентилятора, равный для штампованных лопастей 0.2-0.4 и для литых профилированных лопастей – 0.55-0.65.
Потери на привод вентилятора не должны превышать 5-8% номинальной мощности двигателя.
Похожие статьи:
poznayka.org
Основы расчета жидкостной системы охлаждения
Для расчета системы охлаждения автомобильного или тракторного двигателя исходной величиной является количество отводимого от него в единицу времени тепла Qохл. Это количество может быть определено из уравнения теплового баланса:
,
где qохл – доля количества тепла, отводимого от двигателя. Для бензиновых ДВС qохл = 800–1300 КДж/КВт с, для дизельных ДВС qохл = 1100–1150 КДж/КВт с.
Определив величину Qохл, находят затем количество жидкости, циркулирующей в системе охлаждения в единицу времени,
,
где Сж – теплоемкость циркулирующей жидкости.
Для воды Сж = 4.22 КДж/кг К, для этиленгликолевых смесей Сж = 2–3.8 КДж/кг К;
tвыхж, tвхж – температуры выходящей из радиатора жидкости и входящей в него, °С.
Для радиаторов автомобильных и тракторных двигателей значение tвыхж – tвхж = 5–10 С.
Систему охлаждения двигателя обычно рассчитывают для двух режимов работы двигателя: при номинальной мощности и максимальном крутящем моменте.
Величина поверхности охлаждения радиатора (м2) определяется по формуле:
,
где k – полный коэффициент теплопередачи через стенки радиатора,
tохлж – средняя температура охлаждающей жидкости в радиаторе, °С;
,
где tвхохлж = 90° С – температура охлаждающей жидкости на входе в радиатор;
tвыхохлж = 80–85° С – температура охлаждающей жидкости на выходе из радиатора;
tохлв – средняя температура проходящего через радиатор воздуха, °С,
,
где tвхохлв = 40° С – температура воздуха на входе в радиатор;
tвыхохлв= 60–70°С – температура воздуха на выходе из радиатора.
Коэффициент k зависит от многих факторов: материала охлаждающей решетки, формы и состояния ее внутренней и наружной поверхностей, характера движения воздушного потока и т. д. Теплопередача радиатора значительно ухудшается при образовании в нем накипи, ржавчины или при покрытии грязью.
Величина k может быть определена по формуле:
,
где a 1 = 8500–14500 КДж/м2 ч К – коэффициент теплоотдачи от жидкости к стенкам радиатора;
l – коэффициент теплопроводности металла стенок (трубок) ра-диатора. Для латуни значение = 300–450 КДж/м ч К, для алюминия = 300–350 КДж/м ч К, для нержавеющей стали = 35–70 КДж/м ч К;
b– толщина стенки трубки, м;
a 2 – коэффициент теплоотдачи от стенок радиатора (трубок) к воздуху, = 150–1100 КДж/м2чК.
Коэффициент 2 в основном зависит от скорости воздуха ?воз , проходящего через радиатор, и выражается зависимостью:
.
Для предварительных расчетов площади радиатора системы охлаждения можно использовать формулу:
,
где f – удельная площадь охлаждения, м2/КВт.
Для легковых автомобилей f = 0.14–0.3, для грузовых автомобилей f = 0.2–0.4, для тракторов f = 0.4–0.55.
Емкость системы жидкостного охлаждения л. (Ne в КВт) изменяется в следующих пределах: для легковых автомобилей – (0.13–0.35) Ne, для грузовых автомобилей – (0.27–0.8) Ne, для тракторов – (0.5–1.7) Ne.
Размеры вентилятора автомобильного или тракторного двигателя должны быть таковы, чтобы обеспечить подачу воздуха в количестве, необходимом для охлаждения жидкости в радиаторе.
Тип вентилятора определяют по условному коэффициенту быстроходности:
,
где Vвоз – производительность вентилятора, м3/с.
,
где Vвоз = 1.07 кг/м3 – плотность воздуха;
Своз = 1 КДж/кг К – теплоемкость воздуха;
Н – напор вентилятора. Н = 600–1000 Па.
При nусл = 15–100 используют центробежные вентиляторы, при nусл = 80–300 – осевые одноступенчатые вентиляторы.
Воздушная система охлаждения
В двигателях с воздушным охлаждением для обеспечения нормального теплового состояния двигателя площади наружных поверхностей головок и цилиндров увеличивают путем их оребрения. От поверхности оребрения тепло, поступающее к ней от стенок камеры сгорания и стенок цилиндра, отводится охлаждающим потоком воздуха.
Положительными особенностями системы воздушного охлаждения являются несложное обслуживание, надежность в эксплуатации, меньший по сравнению с системой жидкостного охлаждения вес и простота конструкции, упрощение эксплуатации двигателя в безводных районах, а также устранение опасности замерзания воды в радиаторе и рубашке двигателя (в случае заполнения их водой) при низких температурах.
Схема движения воздуха, охлаждающего однорядный четырехцилиндровый двигатель, представлена на рис. 3.8. Каналы, по которым движется воздух, разделены на участки: входа воздуха, прохождения воздуха через вентилятор 1, распределения воздуха по цилиндрам,прохождения воздуха по межреберным каналам и отводного трубопровода. В рассматриваемой схеме охлаждаемые поверхности находятся на линии нагнетаемого воздуха. В некоторых случаях воздух через межреберные каналы не нагнетается, а просасывается.
Для получения эффективного и равномерного охлаждения при минимальной затрате мощности в двигателях с воздушным охлаждением применяют дефлекторы. Дефлекторы представляют собой направляющие устройства для подачи охлаждающего потока воздуха к оребренным поверхностям с определенными скоростью и направлением.
Рис.
3.8. Схема системы воздушного охлаждения
двигателя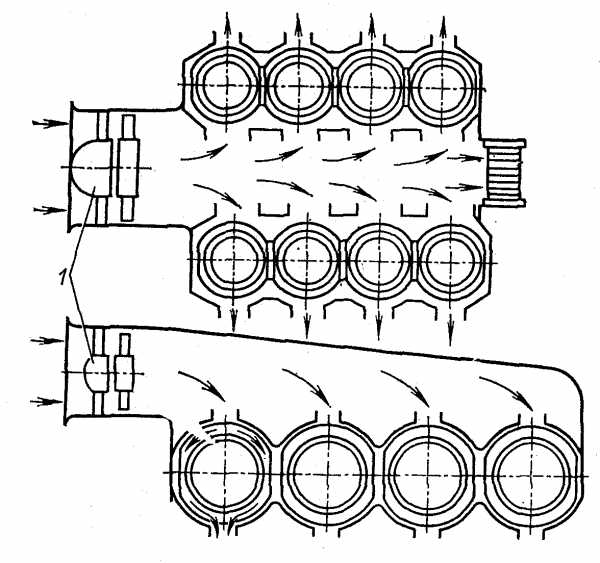
При проектировании системы воздушного охлаждения стремятся обеспечить подачу охлаждающего воздуха в первую очередь к наиболее горячим местам головки цилиндров (перемычки между гнездами клапанов и др.), а также к свечам зажигания (в бензиновых двигателях) и форсункам (в дизелях). Для улучшения теплопередачи поток охлаждающего воздуха должен омывать поверхности охлаждения равномерно и с достаточно высокой скоростью.
Расчет системы воздушного охлаждения автомобильных и тракторных двигателей сводится к определению параметров оребрения двигателя, производительности и размеров вентилятора, а также затрачиваемой на привод вентилятора мощности.
Проведение этого расчета вследствие влияния ряда трудно учитываемых факторов, а также из-за отсутствия данных о взаимозависимости расчетных параметров системы охлаждения весьма сложно и связано с большими трудностями. В особенности сложен теоретический расчет теплопередачи и аэродинамического сопротивления оребрения двигателя. Поэтому на практике при проектировании системы воздушного охлаждения обычно задаются удельной поверхностью оребрения и широко пользуются экспериментальными данными прототипов двигателей.
В начале расчета задаются его исходными параметрами, к которым относятся: а) температура, давление и влажность окружающего двигатель воздуха, б) рабочие температуры деталей двигателя и в) расчетный режим работы двигателя.
В качестве расчетной температуры окружающего воздуха принимают температуру, равную 40 °С.
Превышение рабочих допустимых температур может вызвать нарушение работы (увеличение нагарообразования, коробление головки цилиндра, закоксовывание и зависание иглы форсунки в дизелях, детонацию и калильное зажигание в бензиновых двигателях, повышенный износ цилиндра, поршня и поршневых колец).
Средняя температура у оснований чугунных ребер цилиндров 130–170 °С; у оснований чугунных ребер головки цилиндров 170–220 °С. При алюминиевых сплавах средние температуры соответственно 130–150 и 160–200 °С.
Минимальные температуры внутренних поверхностей цилиндра и его головки стремятся обеспечить не ниже 130–140 °С, т. е. значительно выше точки росы выпускных газов.
studfiles.net
