Нижняя граница 8 дикселя это – Борисов Б.А. Об изменении уровня нижней границы четвертичной системы и уточнении возраста границ ее основных подразделений
Точная верхняя и нижняя границы множеств
Точная верхняя граница (верхняя грань) и точная нижняя граница (нижняя грань) — обобщение понятий максимума и минимума множества соответственно.
Используемые определения
Мажоранта или верхняя грань (граница) множества — число , такое что .
Миноранта или нижняя грань (граница) множества — число , такое что
Определения
Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества упорядоченного множества (или класса) , называется наименьший элемент , который равен или больше всех элементов множества . Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается .
Более формально:
- — множество верхних граней , то есть элементов , равных или больших всех элементов
Точной (наибольшей) нижней гранью (границей), или и́нфимумом (лат. infimum — самый низкий) подмножества упорядоченного множества (или класса) , называется наибольший элемент , который равен или меньше всех элементов множества . Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается .
Замечание
Эти определения ничего не говорят о том, принадлежит ли и множеству или нет.
В случае , говорят, что является максимумом , то есть .
В случае , говорят, что является минимумом , то есть .
Примеры
- На множестве всех рациональных чисел, больших пяти, не существует минимума, однако существует инфимум. такого множества равен пяти. Инфимум не является минимумом, так как пять не принадлежит этому множеству. Если же определить множество всех натуральных чисел, больших пяти, то у такого множества есть минимум и он равен шести. Вообще говоря, у любого непустого подмножества множества натуральных чисел существует минимум[1].
- Для множества
- ; .
- и .
Теорема о гранях
Формулировка
Непустое множество, ограниченное сверху, имеет верхнюю грань, ограниченное снизу — нижнюю грань. То есть существуют и такие, чтоДоказательство
Для множества ограниченного сверху. Пусть — мажоранта множества , представленная в виде бесконечной десятичной дроби. Множество непусто. Запишем все числа из в виде нормальных десятичных дробей,
- .
Множество непусто и ограниченно сверху числом , поэтому существует .
Множество десятичных чисел вида таких, что среди элементов есть число, представление которого в виде бесконечной десятичной дроби начинается с выражения , непусто и состоит не более чем из десяти элементов, поэтому существует .
Допустим, что для некоторого номера построено десятичное число такое, что
- существует элемент , представление которого в виде бесконечной десятичной дроби начинается с выражения
- если x — элемент с представлением , то
- .
Обозначим множество десятичных чисел вида , которые служат начальными выражениями для элементов множества . По определению числа на основании свойства 1 множество непусто. Оно конечно, поэтому существует число , обладающее свойствами 1-2 с заменой на , причем появление -ого знака после запятой не влияет на величины предшествующих знаков.
На основании принципа индукции для любого оказывается определенной цифра и поэтому однозначно определяется бесконечная десятичная дробь
Возьмем произвольное число . По построению числа для любого номера выполняется и поэтому . Следовательно, выполнена верхняя строчка в правой части соотношения 1.1 (смотри формулировку). Следовательно, .
Для множества , ограниченного снизу, рассуждения проводятся аналогично.
Свойства
Вариации и обобщения
Простой Пример
Если множество открытое (граница не принадлежит множеству), например: x<5, то 5 – супремум, но не максимум.
Если множество замкнуто (граница принадлежит множеству), например: x≥2, то 2 – минимум и инфимум одновременно.
Литература
- Богданов Ю. С., Кастрица О. А., Сыроид Ю. Б. Математический анализ: Учебное пособие для вузов. — М.: ЮНИТИ-ДАНА, 2003.- С. 11-14. ISBN 5-238-00500-8
- Богданов Ю. С. Лекции по математическому анализу. Ч. 1. — Мн.: Издательство БГУ, 1974. — С. 3—8.
Примечания
- ↑ Строго говоря, у любого непустого подмножества вполне упорядоченного множества существует в силу принципа фундированности минимум.
dic.academic.ru
Верхняя и нижняя грани множества — ПриМат
Ограниченное сверху числовое множество имеет бесконечно много верхних границ, среди которых особенную роль играет найменьшая из них. Число называется точной верхней гранью (границей), если:
для
для (любое число меньшее M верхней гранью не является).
( — супремум ).
Число называется точной нижней гранью (границей), если:
для
для (любое число меньшее M верхней гранью не является).
( — инфимум ).
(если множество неограничено сверху, то пишем если множество неограничено снизу, то пишем )
Примечание: если не является точной верхней гранью множества и , тогда
если не является точной нижней гранью множества и , тогда
Примеры:
Единственность верхних и нижних точных граней
Если множество имеет и , то он единственный.
Рассмотрим для .
Пусть множество имеет 2 точных верхних грани: и
Допустим .
Так как и , то , что противоречит тому факту, что
Аналогично доказывается единственность нижней точной грани.
Практические задания:
Определить точные нижнюю и верхнюю грани множества рациональных чисел , удовлетворяющих равенству .
Решим неравенство .
Докажем это:
. Так и есть, является верхней границей множества .
;
Действительно, всякие рациональные (и при этом ) будут элементами множества , причём . То есть какое бы рациональное число из мы не взяли, можно взять рациональное число из так, что оно будет находиться ближе к на числовой прямой.
Пусть — множество чисел, противоположных числам
Доказать, что
Пусть — элемент из множества противоположный элементу из множества .
Распишем точную нижнюю грань для множества по определению:
.
Получили:
.
Тоесть: .
Так как , .
Тест “Верхняя и нижняя грани множества”
Лимит времени: 0
Информация
Тестовые вопросы по вышеизложенному материалу.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 5
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)| Средний результат |
|
| Ваш результат |
|
- С ответом
- С отметкой о просмотре
Таблица лучших: Тест “Верхняя и нижняя грани множества”
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Источники:
Конспект по мат.анализу (Лекции Лысенко З.М.)
В.И.Коляда, А.А.Кореновский «Курс лекций по мат.анализу, часть 1» (Одесса «Астропринт» , 2009г.), стр.7.
В.И.Ильин, Э.Г.Позняк «Основы мат.анализа, часть 1, выпуск 2» (Издание четвёртое, переработанное и дополненное, 1982г.) стр.44.
Б.П.Демидович «Сборник задач и упражнений по мат.анализу» (издание пятое) стр.12. №17, 19а.
Подробнее на:
sernam.ru
Wikipedia
Поделиться ссылкой:
Похожее
ib.mazurok.com
1.2. Границы числовых величин
Наряду с понятиями абсолютной, относительной погрешности и их оценок, в теории погрешности используются и другие понятия, позволяющие оценивать качество приближенных значений числовых величин. Это границы величин. Рассмотрим их.
Пусть имеется числовая величина
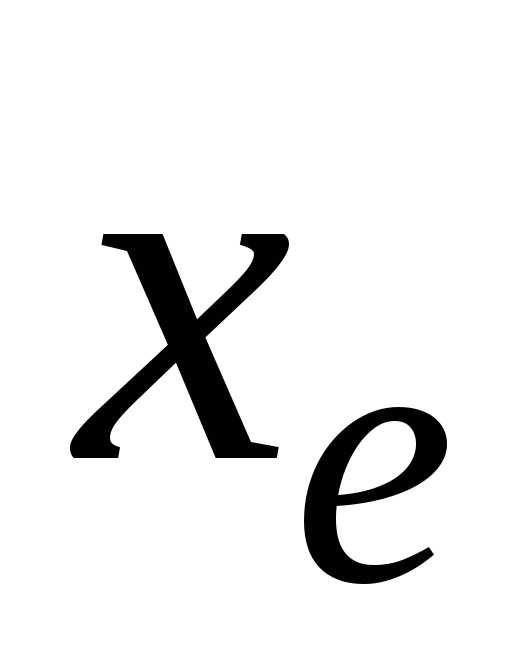 неизвестно, но имеется некоторая
информация о нем, позволяющая определить
ограниченное множество принадлежности
неизвестно, но имеется некоторая
информация о нем, позволяющая определить
ограниченное множество принадлежности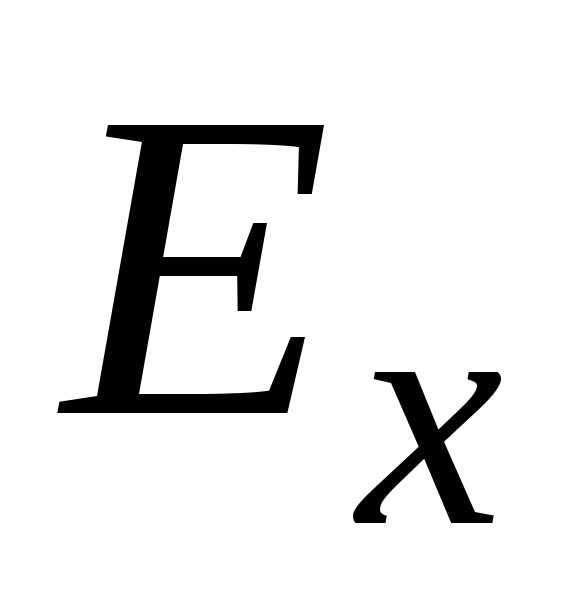 точного значения величиныx (
точного значения величиныx ( ).
Множество
).
Множество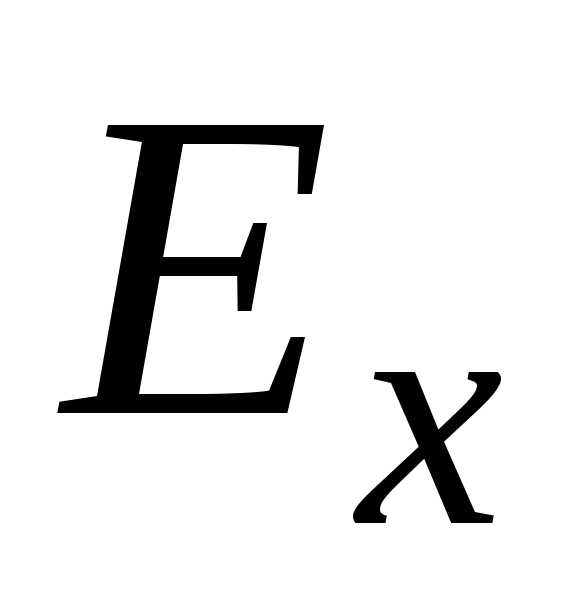 ,
как и всякое ограниченное множество
имеет границы: верхние и нижние.
,
как и всякое ограниченное множество
имеет границы: верхние и нижние. Верхней (нижней)
границей величины x называется любая из верхних (нижних)
границ множества 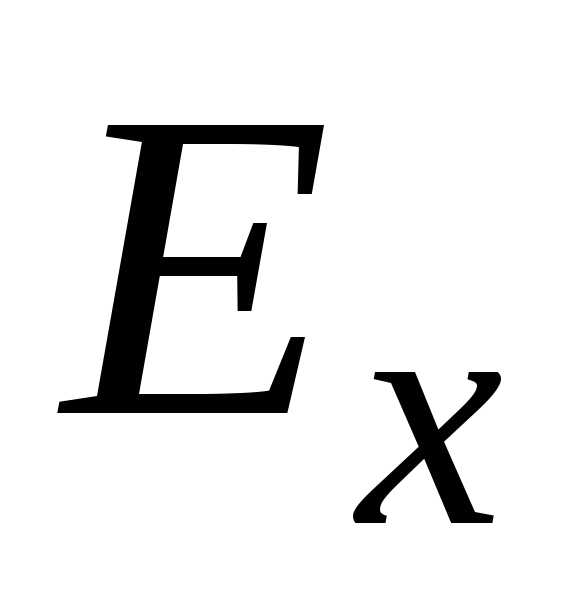 .
Обозначение:
.
Обозначение: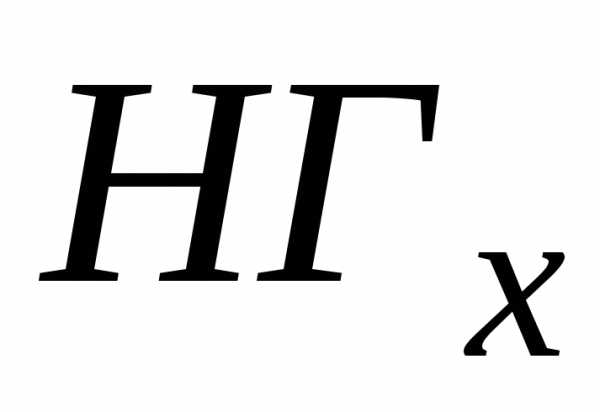 –
любая нижняя граница величиныx,
–
любая нижняя граница величиныx, 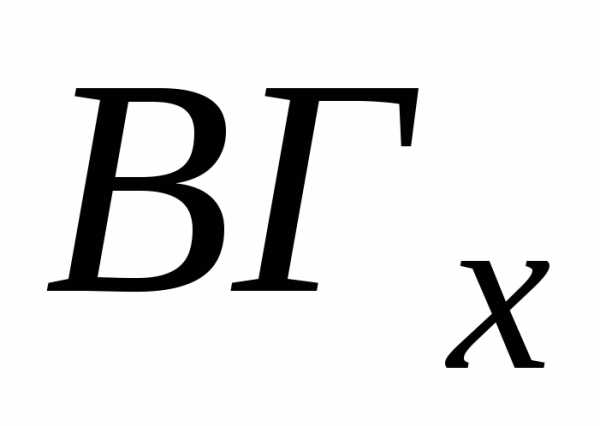 –
любая верхняя граница величиныx.
–
любая верхняя граница величиныx.
Наименьшую из верхних границ назовем точной верхней границей величины x, а наибольшую из нижних границ назовем точной нижней границей величины x. Таким образом, точные границы величины x представляют собой
, . (1.2.1)
Какие бы границы величины x ни выбирались (точные или не точные), для них должно быть справедливо отношение
, (1.2.2)
откуда следует, что
. (1.2.3)
Понятие границы
величины x тесно связано
с понятиями приближенного значения 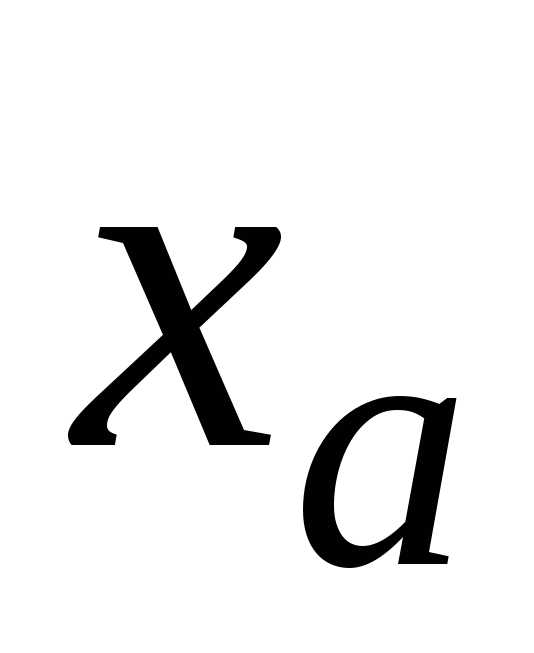 и оценки его погрешности
и оценки его погрешности 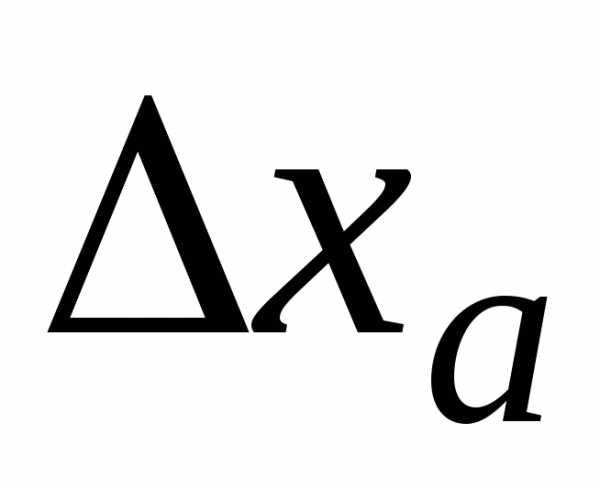 .
Зная
.
Зная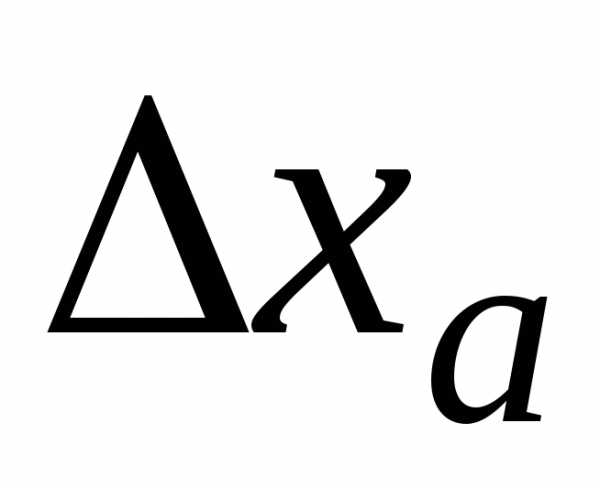 ,
всегда можно найтии
,
всегда можно найтии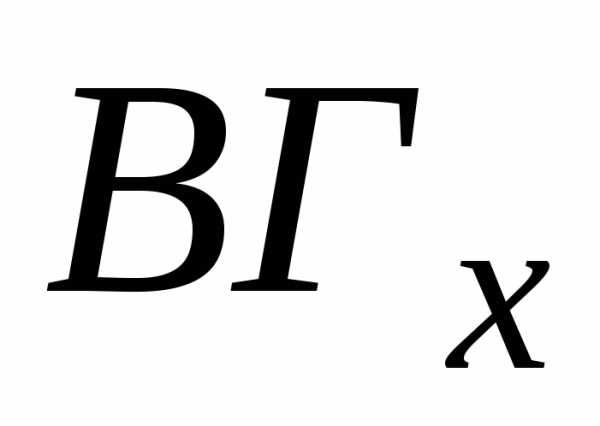 .
А зная
.
А зная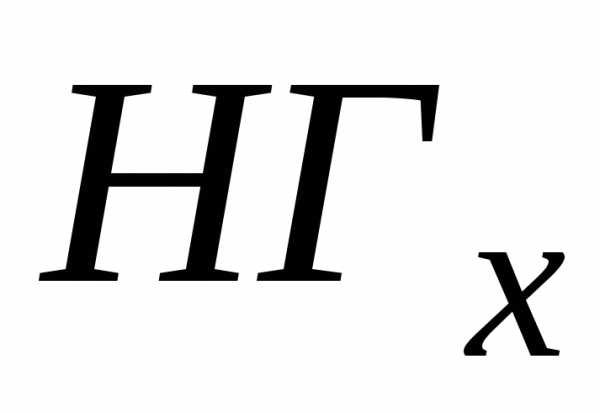 и
и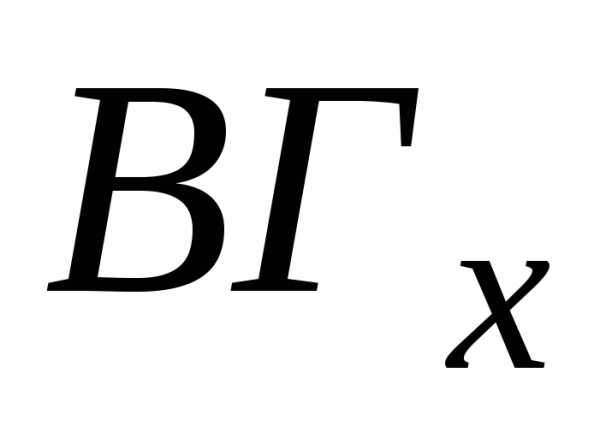 ,
можно выбрать
,
можно выбрать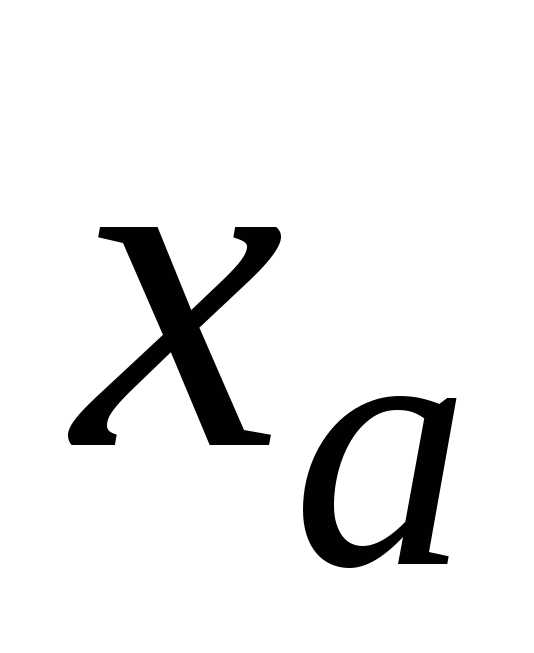 и найти для него
и найти для него .
Рассмотрим как это делается.
.
Рассмотрим как это делается.
Пусть известны
приближенное значение  величиныx и
оценка его погрешности
величиныx и
оценка его погрешности 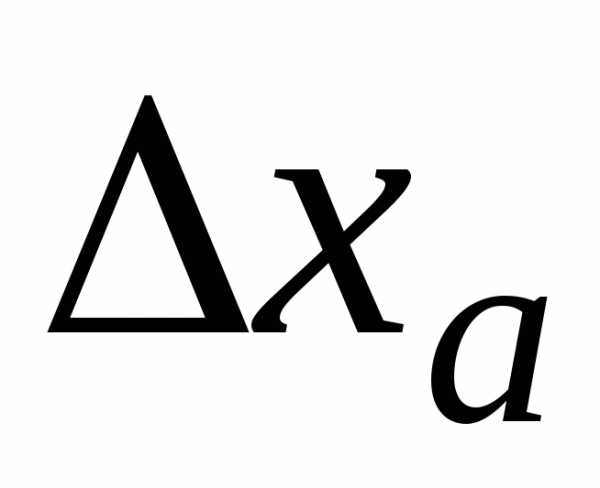 .
Найдем границы этой величины. Решив
неравенство (1.1.2) относительно
.
Найдем границы этой величины. Решив
неравенство (1.1.2) относительно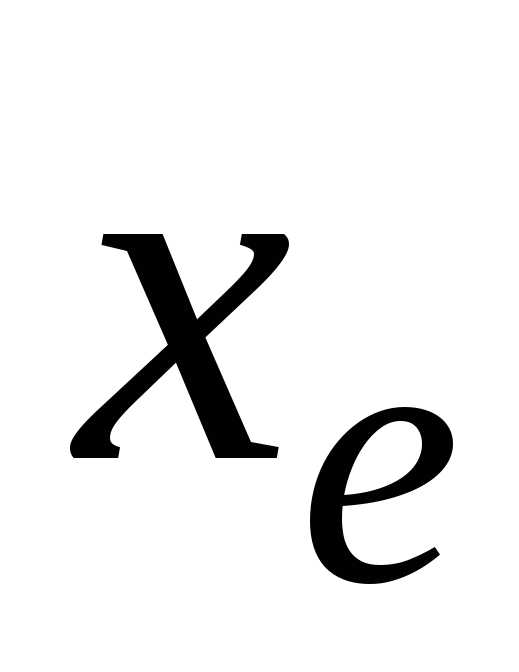 получим
получим
или .
Мы использовали всю имеющуюся информацию о точном значении величины, поэтому
.
Отсюда получим точные границы величины x
(1.2.4)
Рассмотрим теперь
обратную задачу. Пусть известны границы
величины x: 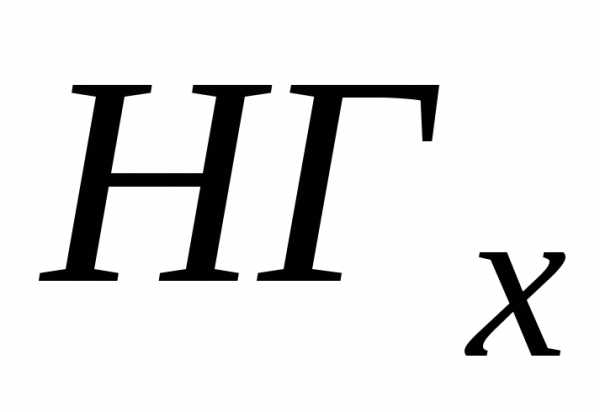 ,
,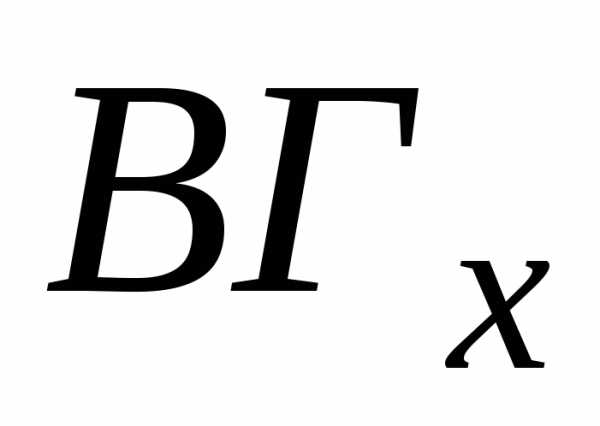 .
Выберем приближенное значение величины
.
Выберем приближенное значение величины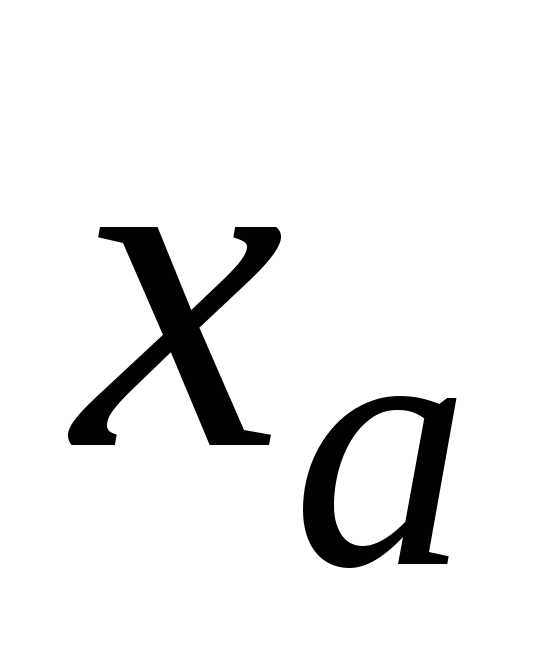 такое,
чтобы предельная абсолютная погрешность
его была наименьшей из возможных. Никакой
информации о точном значении величиныx,
кроме значений
такое,
чтобы предельная абсолютная погрешность
его была наименьшей из возможных. Никакой
информации о точном значении величиныx,
кроме значений 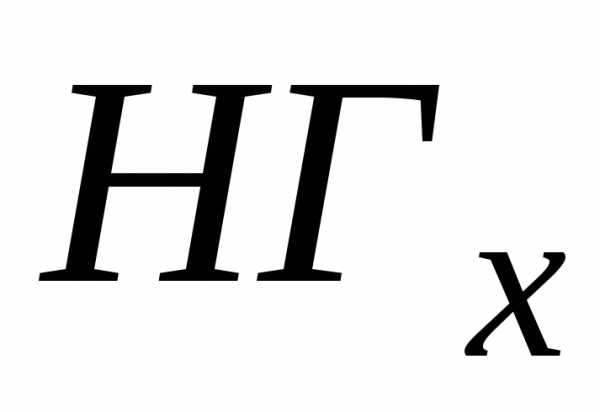 и
и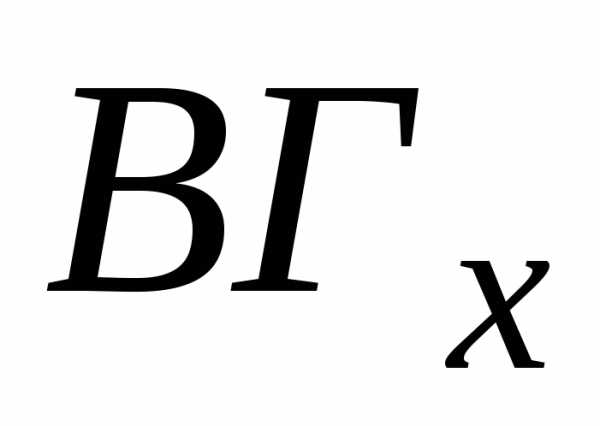 у нас нет. Поэтому из отношения (1.2.2)
следует, что.
Далее, согласно результатам примера 1
из параграфа 1.1, приближенное значение
величины
у нас нет. Поэтому из отношения (1.2.2)
следует, что.
Далее, согласно результатам примера 1
из параграфа 1.1, приближенное значение
величины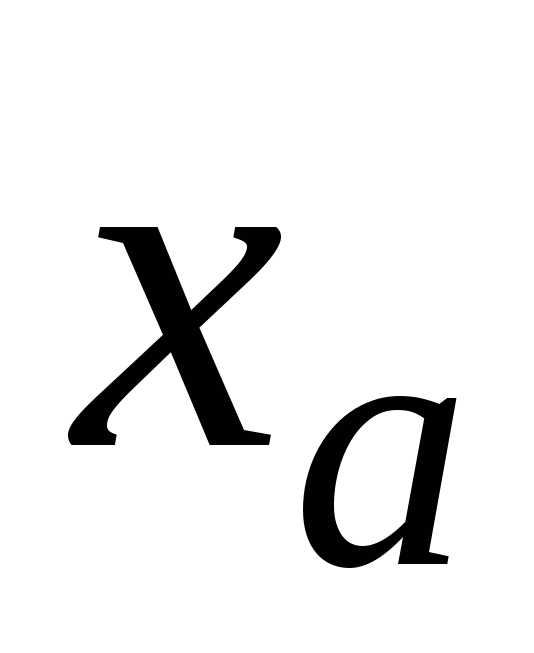 следует выбрать совпадающим с серединой
отрезка:
следует выбрать совпадающим с серединой
отрезка:
 .
(1.2.5)
.
(1.2.5)
Тогда его предельная абсолютная погрешность будет самой маленькой и равной
. (1.2.6)
Формулы (1.2.5),
(1.2.6) могут быть формально получены, если
решить систему (1.2.4) относительно
переменных 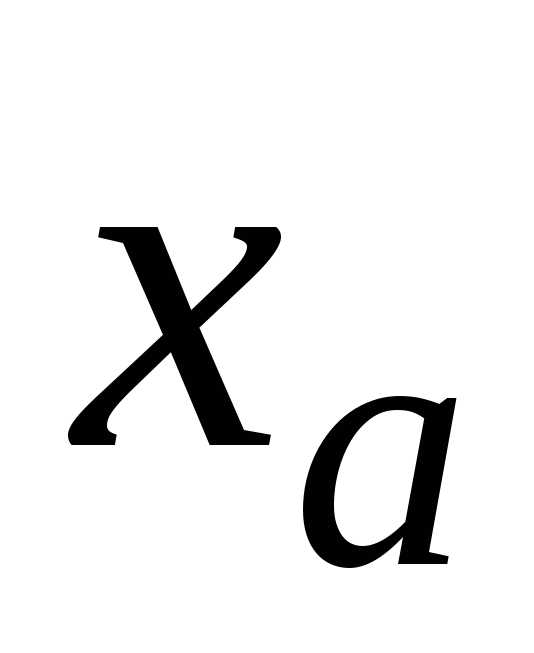 и
и .
.
Рассмотрим теперь
обратную задачу. Пусть известны границы
величины x: 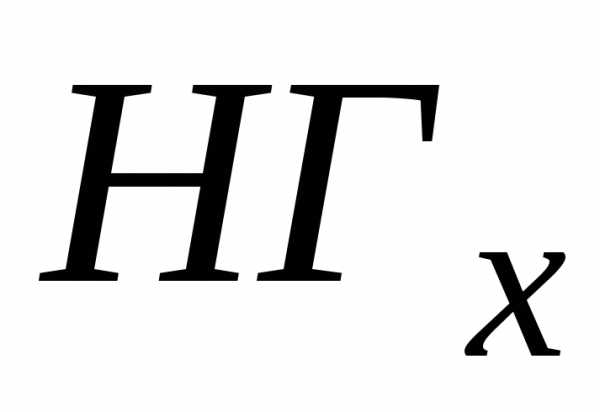 ,
,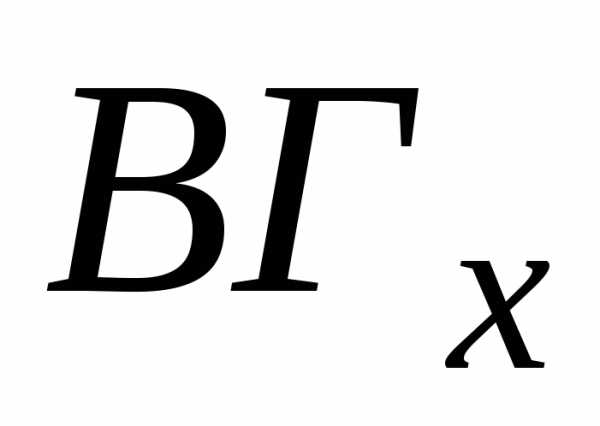 .
Выберем приближенное значение величины
.
Выберем приближенное значение величины такое,
чтобы предельная абсолютная погрешность
его была наименьшей из возможных
значений. Никакой информации о точном
значении величиныx,
кроме значений
такое,
чтобы предельная абсолютная погрешность
его была наименьшей из возможных
значений. Никакой информации о точном
значении величиныx,
кроме значений 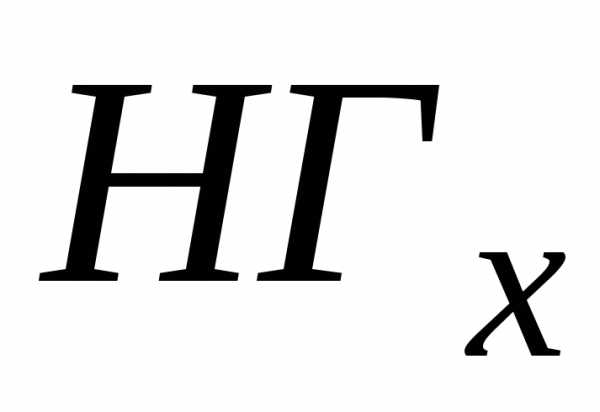 и
и ,
у нас нет. Поэтому из отношения (1.2.2)
следует, что.
Далее, согласно результатам примера из
параграфа 1.1, приближенное значение
величиныследует выбрать совпадающим с серединой
отрезка:
,
у нас нет. Поэтому из отношения (1.2.2)
следует, что.
Далее, согласно результатам примера из
параграфа 1.1, приближенное значение
величиныследует выбрать совпадающим с серединой
отрезка:
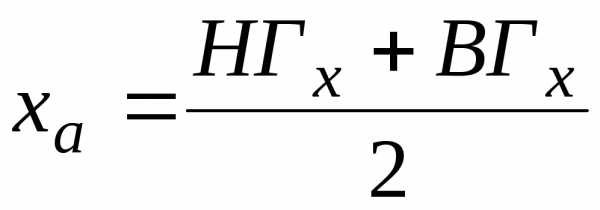 .
(1.2.7)
.
(1.2.7)
Тогда его предельная абсолютная погрешность будет самой маленькой и равной
. (1.2.8)
Формулы (1.2.7),
(1.2.8) могут быть формально получены, если
решить систему (1.2.4) относительно
переменных  и
и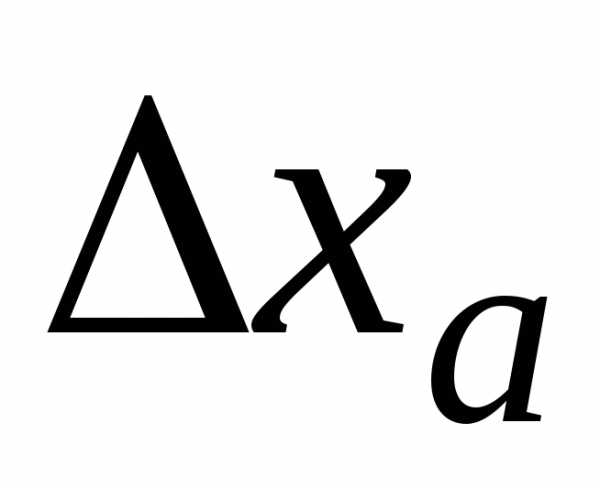 .
.
studfiles.net
|
В связи с ратификацией Исполнительным комитетом Международного союза геологических наук (МСГН) рекомендаций Международной комиссии по стратиграфии (МКС) о понижении нижней границы четвертичной системы (квартера) и соответственно основания плейстоценового отдела на уровень 2,588 млн. лет предложен актуализированный проект Обшей стратиграфической шкалы квартера, сопоставленный с международной шкалой этой системы и кислородно-изотопной шкалой. Ключевые слова: четвертичная система, плейстоцен, эоплейстоцен, неоплейстоцен, ярусы гелазий, калабрий, ионий, тарантий, голоцен
В августе 2008 г. на 33-й сессии Международного геологического конгресса (Норвегия) подтвержден самостоятельный статус четвертичной системы (квартера) с нижней границей 1,8 млн. лет (в основании калабрия), принятой в 1998 г . в Общей стратиграфической шкале. На конгрессе проблемы, связанные с квартером и неогеном, разбирались на семинаре «Плиоцен-четвертичные корреляции и глобальные изменения» и на специально созванном совещании «Переосмысление квартера и плейстоцена: открытая дискуссия». В центре внимания участников были различные варианты уровня нижней границы четвертичной системы, например в основании гелазия, а также вопросы по структуре системы, в том числе по её ярусному делению [Гладенков, 2009]. В июле 2009 г . Исполнительный комитет МСГН ратифицировал предложение МКС относительно определения нижней границы четвертичной системы/периода (и верхней границы неогеновой системы/периода) и изменения нижней границы плейстоценового отдела/эпохи, утвердив следующие рекомендации МКС: 1) нижняя граница плейстоценового отдела/эпохи должна быть понижена так, чтобы плейстоцен включал ярус/век гелазий и его нижняя граница определялась точкой глобального стратотипа границы (ТГСГ) Монте Сан Никола (Сицилия, Италия), которая также определяет основание гелазия; 2) нижняя граница четвертичной системы/периода и соответственно граница неогена – квартера формально определяется ТГСГ Монте Сан Никола и таким образом совпадает с основанием плейстоцена и гелазия; 3) в соответствии с этим ярус/век гелазий перемещается из плиоценового отдела/эпохи в плейстоцен (IUGS-Bulletin. N41, July 2009). В июле 2009 г . МКС на сайте Подкомиссии по стратиграфической информации опубликовала перечень ТГСГ кайнозойской эры с уточненными возрастами нижних границ ярусов, в том числе и оснований ярусов позднего кайнозоя (снизу вверх): гелазийского (гелазий) – 2,588, калабрийского (калабрий) – 1,806, ионийского (ионий) – 0,781, тарантского (тарантий) – 0,126 и голоценового (голоцен) – 0,011784 млн. лет. На основании изложенного предлагается актуализированный проект Общей стратиграфической шкалы четвертичной системы (таблица), в котором учтены последние решения МСГН и МКС по квартеру. Левую часть таблицы занимает Международная стратиграфическая шкала четвертичной системы. Звездочкой отмечены ярусы гелазий, калабрий, голоцен, ратифицированные Исполнительным комитетом МСГН, остальные (ионий, тарантий) находятся на разных стадиях рассмотрения. В проект Общей стратиграфической шкалы четвертичной системы, в отличие от утвержденной ОСШ этой системы ( 2007 г .), введены ярусы. В связи с присоединением гелазия предложено трехчленное деление эоплейстоцена. Кислородно-изотопная шкала [Bassinot et al., 1994] помещена здесь, как и ранее [Постановления…, 2008], для возрастной привязки утвержденных на бюро МСК в 2007 г . ступеней неоплейстоцена. При сравнении возраста нижних границ ярусов с основаниями стадий кислородно-изотопной шкалы отмечены незначительные различия: гелазий – 8, калабрий – 6, ионий – 6, тарантий – 1 и голоцен – 0,784тыс. лет. В целях устранения этих различий, по-видимому, целесообразно внести соответствующие изменения (уточнения) в Кислородно-изотопную шкалу (таблица), за исключением основания 19-й стадии, поскольку подошва иония определена по границе палеомагнитных зон Брюнес-Матуяма, которая проходит примерно близ кровли нижней трети этой стадии.
Выбранные возрастные границы ярусов и звеньев эоплейстоцена и неоплейстоцена достаточно обоснованы и хорошо коррелируются. Стратотип нижней границы гелазия – разрез Монте Сан Никола (Сицилия) – утвержден в 1996 г . [Rio et al., 1998]. На этом уровне располагаются граница между палеомагнитными ортозонами Матуяма-Гаусс и основание 103-й кислородно-изотопной стадии. Гелазийскому веку соответствует нижнее звено эоплейстоцена. С отложениями этого времени связана фауна млекопитающих хапровского и нижней части псекупского комплексов. Стратотип нижней границы калабрия – разрез Врика (Италия) – утвержден в 1985 г . [Aguirre & Pasini, 1985]. Эта граница проходит близ кровли палеомагнитной субзоны Олдувей и совпадает с основанием 63-й кислородно-изотопной стадии. Калабрийскому веку отвечает среднее и верхнее звенья эоплейстоцена. Граница между звеньями совпадает с основанием палеомагнитной субзоны Кобб-Маунти (1,240 млн. лет). С отложениями среднего звена связана фауна млекопитающих верхней части псекупского комплекса, а с верхним звеном – таманского комплекса. Стратотипы нижней границы иония, предложенные Италией и Японией, находятся в стадии рассмотрения. В обоих стратотипах эта граница проходит между двумя палеомагнитными ортозонами Брюнес-Матуяма (на уровне 781 тыс. лет). Ионийскому веку соответствуют нижнее и среднее звенья неоплейстоцена. Границу между этими подразделениями на уровне 420 тыс. лет фиксирует палеомагнитная субзона Эмперор. Для нижнего звена характерна фауна млекопитающих тираспольского комплекса, а для среднего – сингильского, хазарского и раннемамонтового комплексов. Стратотип нижней границы тарантия (Амстердам, Нидерланды) прошел апробацию в МКС и направлен на ратификацию в МСГН [Clague, 2008]. Тарантскому веку соответствует верхнее звено неоплейстоцена и фауна млекопитающих мамонтового комплекса. С началом тарантия связана палеомагнитная субзона Блейк (~120 тыс. лет). Стратотип нижней границы голоцена установлен в Центральной Гренландии и утвержден в 2008 г. [Clague, 2008; Walker et al., 2009]. Близ этого уровня располагается маркирующий горизонт, наблюдаемый, кроме Гренландии, в Северной Европе и известный под названием «ведде-пепел» с возрастом 10400-10300 радиоуглеродных лет или примерно 12 000 календарных лет. Образование пеплового горизонта связано с извержением и ныне действующего вулкана Катла на юге Исландии. Пепловые частицы извержения этого вулкана по геохимическим данным установлены также в позднедриасовых отложениях к северу от Санкт-Петербурга в акватории озер Медведское и Пасторское. В разрезах обоих озер нижняя граница голоцена проходит между отложениями дриаса и пребореала [Субетто и др., 2002]. Примерно на этом уровне зафиксирована палеомагнитная микрозона Гетеборг (12 тыс. лет). Предлагаемый новый актуализированный проект Общей шкалы четвертичной системы позволяет максимально сблизить её с Международной шкалой квартера и в то же время сохранить без изменений существующую систему выделения и геологического картирования подразделений неоплейстоцена, сопоставленных со стадиями кислородно-изотопной шкалы. Для неоплейстоценовой эпохи квартера, в течение которой оледенения периодически чередовались с межледниковьями, эта шкала служит надежным эталоном для климатостратиграфических построений. Что же касается эоплейстоценовой эпохи, то для её детализации ведущей является биостратиграфическая основа, однако и здесь климатостратиграфические методы во многих случаях играют важную роль, особенно для целей корреляции и одинакового подхода к выделению основных подразделений этой эпохи.
ЛИТЕРАТУРА 1. Гладенков Ю.Б. Позднекайнозойские экосистемы и основания для пересмотра статуса и границ неогена и квартера // Актуальные проблемы неогеновой и четвертичной стратиграфии и их обсуждение на 33-м Международном геологическом конгрессе (Норвегия, 2008 г.): Материалы Всероссийского научного совещания (Москва, 2009 г .). – М.: Геос. 2009. С. 8-14. 2. Постановления Межведомственного стратиграфического комитета и его постоянных комиссий. – СПб.: Изд-во ВСЕГЕИ, 2008. Вып. 38. – С. 121-122. 3. Субетто Д.Л., Давыдова Н.Н., Сапелко Т.В. и др. Палеоклимат на Карельском перешейке на рубеже позднего плейстоцена и голоцена по данным изучения оз. Медведского // Известия РГО. СПб.: Наука, 2002. Т. 134. Вып. 1. С. 47-64. 4. Aguirre E., Pasini G. The Pliocene-Pleistocene Boundary // Episodes. 1985. Vol. 8. N. 2. P. 116-120. 5. Bassinot F.С., Labery L.D., Vinsent E. et al. The astronomical theory of climate and the age of the Brunhes – Matuyama magnetic reversal // Earth and Planet. Sci. Let. 1994. Vol. 126. P. 91-108. 6. Clague J.J. Importance of Quaternary research to society // Episodes. 2008. Vol. 31. N 2. P. 203-206. 7. Rio D., Sprovieri R., Castradori D., De Stefano E. The Gelasian Stage (Upper Pliocene): A new unit of the global standard chronostratigraphic scale // Episodes. 1998. Vol. 21. N 2. P. 82-87. 8. Walker M., Johnsen S., Rasmussen S.O., Popp T. et al. Formal definition and dating of the GSSP (Global Stratotype Section and Point) for the base of the Holocene using the Greenland NGRIP ice core, and selected auxiliary records // Quaternary Sci. 2009. Vol. 24. Is. 1. P. 3-17.
Due to ratification of recommendations of the International Commission on Stratigraphy on lowering of the lower Quaternary boundary and substantiation of Pleistocene Series at the level of 2.588 Ma by the Executive Committee of the International Union of Geological Sciences, an updated draft of General Stratigraphic Scale of the Quaternary correlated with the International Scale of this system and Oxygen-isotope Scale is proposed. Key words: Quaternary System, Pleistocene, Eopleistocene, Neopleistocene; stages Gelasian, Calabrian, Ionian, Tarantian, Holocene
|
evgengusev.narod.ru
Индикатор Wilder’s RSI: раздвигаем временные рамки
Индекс относительной силы (RSI) является популярным среди трейдеров индикатором. Но как узнать, сколько баров учитывать при его расчете и как определять верхнюю и нижнюю зоны? В данной статье будет предложен один из способов.
В вышедшей в 1978 году книге “Новые концепции систем технического трейдинга” Дж. Уеллес Уайлдер описал несколько новых индикаторов, включая индекс относительной силы RSI. С момента своего появления, индикатор RSI получил широкое распространение и завоевал популярность среди трейдеров на рынке акций. Сам Уайлдер указывал на несколько преимуществ RSI, наиболее важным из которых он считал нормированную шкалу от 0 до 100.
Но при использовании RSI нужно найти ответы на два важных вопроса:
- Каковы значения верхнего и нижнего уровня индикатора?
- Как для конкретного используемого таймфрейма выбрать правильное число баров, участвующих в расчете RSI?
По поводу первого вопроса, Уайлдер придерживался мнения, что значение 70 свидетельствует о появлении в ближайшем будущем точки разворота тренда вниз. Этот сигнал усиливается, если дополнительно наблюдается расхождение между RSI и ценой. И наоборот, значение RSI 30 свидетельствует о появлении в ближайшем будущем точки разворота вверх. Расхождение с ценой также усиливает сигнал. Уровни 70 и 30 встроены в большинство современных торговых платформ как значения по умолчанию и часто интерпретируются как перекупленность или перепроданность, соответственно. Но сам Уайлдер никогда не использовал термины перекупленности и перепроданности. На самом деле, они имеют смысл только при ненаправленном или колеблющемся в рейндже рынке. Сильные ценовые тренды – напротив, могут оставаться перекупленными или перепроданными в течение длительного времени.
Что касается правильных временных рамок, то Уайлдер предлагал использовать 14-барный RSI. Именно этот вариант принят по умолчанию большинством торговых платформ. Причина, по которой Уайлдер выбрал 14 баров, неизвестна. Почему не 8, 25 или 55 баров? Наиболее вероятной причиной такого выбора явилось то, что в то время он торговал на товарных биржах. Несмотря на популярность его индикаторов на рынке акций, редко кто обращает внимание, что большинство графиков в его книге взяты с товарных рынков, например, контракты на серебро. Графиков, иллюстрирующих применение RSI для акций, нет. Товарные трейдеры, как правило, используют короткие временные рамки – порядка 4-6 недель, а 14 дневных баров – это половина 28-дневного цикла, охватывающего около 5.5 недель. Но каковы бы ни были мотивы Уайлдера, 14 баров зачастую оказываются не лучшим временным диапазоном для многих трейдеров и инвесторов работающих на акциях. В данной статье будет рассмотрено влияние изменения временных рамок на границы доверительного интервала RSI.
Замечания по вычислению RSI
Уайлдер приводит такую формулу для RSI:
Уравнение 1:
RSI = 100 – 100 / (1+RS), где RS – это отношение:
(сумма изменений цены повышающихся дней за период 14 дней/14)/(сумма изменений цены понижающихся дней за период 14 дней/14)
Этот метод не вычисляет истинное среднее арифметическое при определении значения RSI. Если имеются 14 дневных баров, то количество повышающихся и понижающихся дней в сумме должно равняться 14, а по отдельности – быть меньше 14. Например, может быть 8 повышающихся и 6 понижающихся дней. В этом случае, чтобы получить истинное среднее значение, нужно было бы делить сумму изменений повышающихся дней на 8, а сумму изменений понижающихся дней – на 6. Причиной, по которой Уайлдер не вычислял истинное среднее значение, могло стать его желание использовать экспоненциальное сглаживание и уменьшить количество ценовых данных. На самом деле, RS – это отношение суммы изменений цены повышающихся дней к сумме изменений цены понижающихся дней (SUMUP/SUMDN). Это соотношение не изменится, если числитель и знаменатель разделить на 14. Поскольку RSI Уайлдера основывается на изменении цены закрытия дневных баров, то он является индикатором моментума цены.
Зная, что RS – это (SUMUP/SUMDN), можно подставить данное выражение вместо RS в уравнение Уайлдера:
RSI = 100 – 100 / (1 + SUMUP / SUMDN) = 100 * [(1 + SUMUP / SUMDN) – 100] / (1 + SUMUP / SUMDN)
Раскрыв скобки, в числителе получим: 100 + 100 * (SUMUP / SUMDN) – 100. Члены 100 взаимно уничтожаются, и уравнение принимает вид:
RSI = 100 * (SUMUP / SUMDN) / (1 + SUMUP / SUMDN)
Умножив верхнюю и нижнюю части на SUMDN, получаем:
RSI = 100 * SUMUP / (SUMDN + SUMUP) или
Уравнение 2:
RSI = 100 * SUMUP / (SUMUP + SUMDN)
Определение доверительного интервала индикатора RSI
Из уравнения 2 видно, что RSI – это отношение изменения цены закрытия повышающихся дней к изменению цены закрытия всех дней. Значение RSI 75 означает, что 75% всех изменений цены имели место на повышающихся днях. Это значит, что RSI = 75 можно преобразовать в вероятность 0.75 и применять нормальное распределение вероятностей для оценки различных доверительных интервалов.
Доверительные интервалы широко используются в науке, медицине, технике и других сферах. Предположим, что среди нормального мирового населения среднее систолическое кровяное давление составляет 120 мм рт.ст, а стандартное отклонение равно 8 мм рт.ст. При нормальном распределении населения, 95%-й доверительный интервал составил бы 1.96 стандартного отклонения по каждую сторону от среднего значения. В данном примере среднее значение составит примерно от 104 до 136 мм рт. ст. Таким образом, 2.5% нормального населения остаются за пределами доверительных интервалов по обе стороны от среднего значения. Если взять случайную выборку из 100 человек, среди которых лиц с систолическим давлением выше 136 окажется 0.35 или 35%, то это не будет соответствовать выборке, взятой из нормального населения.
Чтобы вычислить стандартное отклонение пропорции, можно использовать:
Уравнение 3:
Стандартное отклонение (SD) = SQRT(p*(1–p)/n)
где:
р – вероятность того, что событие произойдет, (1-р) – вероятность того, что событие не произойдет,
n – количество попыток.
Для выборки из 100 человек, 95%-й доверительный интервал (CI) составляет 1.96 стандартного отклонения с каждой из сторон измеренной пропорции, равной 0.35. Вероятность р равна 0.35, а вероятность (1-р) равна 0.65. Поэтому, стандартное отклонение равно 0.048; а 95%-й доверительный интервал составляет от 0.257 до 0.443.
Мы уже знаем, что у нормальных лиц среднее значение составляет 120, а стандартное отклонение – 8. Поэтому, 2.5% населения будут иметь систолическое кровяное давление 136 и выше. Р=0.025 значительно ниже нижней границы доверительного интервала, равной 0.257. Поэтому выборка из 100 человек, по всей видимости, была сделана не из населения с нормальным кровяным давлением.
Ту же процедуру применим к RSI. Можно ожидать, что при очень большой выборке (n > 10 000) RSI примерно будет равен 50, что даст нам ожидаемое значение 0.5. Допустим, мы измерили выборку из 14 баров и получили RSI=65. Существенно ли это отличается от ожидаемого значения 50?
Используем уравнение 3:
– стандартное отклонение (SD) = SQRT(p*(1–p)/n) = SQRT(0.5*0.5/14) = 0.134
– 95% CI RSI(14) = 0.50 – 1.96*0.134 = 0.2374 [нижняя граница] и 0.50 +1.96 * 0.134 = 0.7626 [верхняя граница]
Применительно к RSI, доверительный интервал имеет значения от 23.74 до 76.26.
Поскольку измеренное значение 65 не выходит за границы доверительного интервала, то оно не существенно отличается от 50. Предположим, что мы измерили еще одну выборку из 14 баров и получили RSI = 80. Это значение лежит вне пределов доверительного интервала и поэтому, скорее всего, может считаться отличным от ожидаемого RSI = 50.
Предположим, что мы хотим найти 90%-й доверительный интервал (отбросив по 5% с каждой стороны) вместо 95%-го для 14-барного RSI. 90%-й интервал ограничен 1.645 SD с каждой стороны от ожидаемого значения:
0.50 – 1.645 * 0.134 = 0.2802 или RSI = 28.02 (нижняя граница)
0.50 + 1.645 * 0.134 = 0.7198 или RSI = 71.98 (верхняя граница)
Любой 14-барный RSI менее 28.02 или больше 71.98 имеет вероятность p < 0.05, т.к. с каждой стороны 5% его распределения находятся за пределами 1.645 стандартного отклонения от среднего значения.
Таким образом, 90%-й доверительный интервал CI для RSI любого количества баров n можно вычислить:
Уравнение 4:
0.5 – SQRT(0.25/n)*1.645 (нижний CI) и 0.5 + SQRT(0.25/n)*1.645 (верхний CI)
Можно сделать несколько очевидных выводов:
- Можно определить доверительные интервалы для RSI, использовав 50 в качестве ожидаемого значения RSI и вычислив стандартное отклонение этой пропорции.
- Границы доверительного интервала зависят от числа попыток или числа баров. Увеличение числа попыток сверх 14 уменьшает границы доверительного интервала, а уменьшение числа попыток менее 14 значительно увеличивает границы доверительного интервала.
- При увеличении количества баров до бесконечности, границы доверительного интервала сходятся на 50, как и следовало ожидать.
Рисунок 1
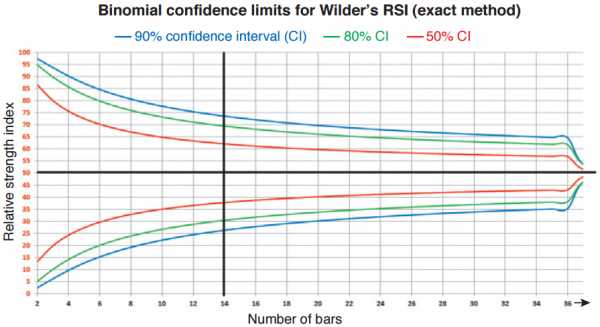
На рисунке 1 представлены границы доверительного интервала для разного числа баров RSI. 90%-й доверительный интервал важен, поскольку он отбрасывает по 5% с каждой стороны, а это – наиболее широко распространенный статистический стандарт значимости в одностороннем критерии гипотезы.
Рисунок 2
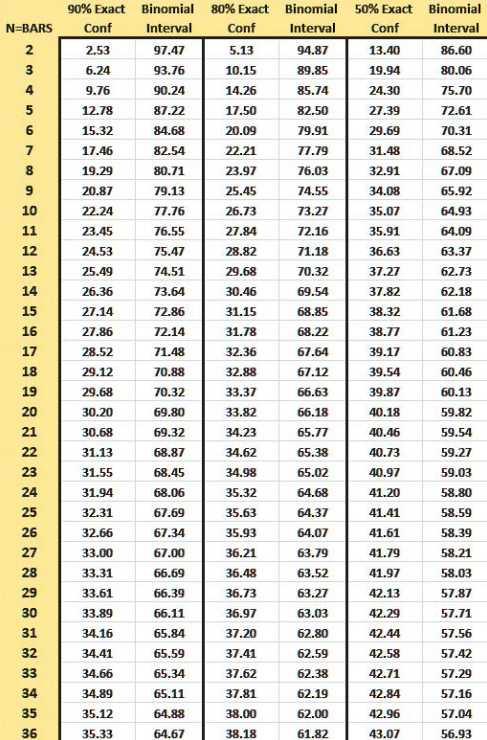
В таблице на рисунке 2 приведены точные значения для границ 90%-го доверительного интервала при различном количестве баров – от 2 до 36. Эти цифры немного отличаются от результатов, которые можно получить из уравнения 4 для значений n < примерно 30. Значения для числа баров более 36 можно вычислить, используя уравнение 4. Как можно видеть из рисунка 1, 14-барный RSI имеет значения границ 90%-го доверительного интервала чуть менее 27 и чуть более 73. Эти значения близки к границам Уайлдера 70/30, что означает, что в нейтральном рыночном окружении чуть больше 5% дней будут находиться выше 70, и чуть больше 5% дней – ниже 30. Для 9-барного RSI и 90%-го доверительного интервала, границы пришлось бы расширить до 21 и 79. Аналогично, для 25-барного RSI и 90%-го доверительного интервала, границы находятся примерно на 32 и 68.
Тестирование индикатора RSI на истории
Используя огромное количество акций из индекса S&P 500, на базе сканера StockChart.com, написан скан со следующим кодом:
[группа = SP500] или [группа = SP600] или [группа = SP400] и [RSI(n) < нижняя граница]
или
[группа = SP500] или [группа = SP600] или [группа = SP400] и [RSI(n)> верхняя граница]
где n – число баров, а верхняя и нижняя границы соответствуют 90%-му доверительному интервалу.
Этот скан был использован в понедельник каждой недели за примерно 4 последних года, т.е. около 200 недель. На несмещенном рынке и при достаточно большой выборке, примерно 5% акций будут находиться выше верхней границы, и примерно 5% – ниже нижней. Это означает, что, в среднем, после нескольких выборок, можно получить около 75 акций на каждом конце доверительного интервала. В противном случае, возможно, вы имеете дело с выборкой, отличной от нормальной. Давайте посмотрим, как теоретическая конструкция соотносится с реальностью.
Рисунок 3
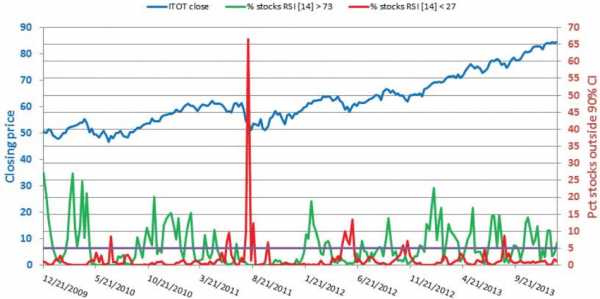
На рисунке 3 вы видите графическое представление результатов – процент от 1500 акций для 14-барного RSI. Математическое ожидание процента акций, находящихся за верхней границей в течение этого 202-недельного периода, составило 5.14%, а медианное значение – 3.5%. Для нижней границы доверительного интервала, математическое ожидание процента акций, находящихся за ее пределами, составило 1.74%, а медианное значение – 0.7%.
Рисунок 4
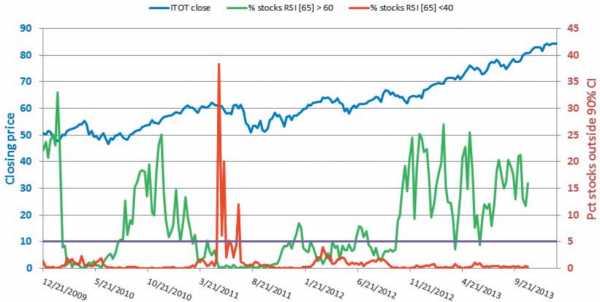
На рисунке 4 вы видите графическое представление результатов – процент от 1500 акций для 65-барного RSI, для того же самого 202-недельного периода. Для верхней границы доверительного интервала, математическое ожидание составило 8.35%, а медианное значение – 5.07%. Для нижней границы доверительного интервала, математическое ожидание составило 1.04%, а медианное значение – 0.4%.
Понятно, что рынок в этот период имел смещение вверх, что продолжается с 15 марта 2010 по настоящий момент. Об этом свидетельствует то, что, в среднем, более 5% акций находились выше верхней границы доверительного интервала для 14-барного и 65-барного случаев, в то время как намного меньше 5% акций находились ниже нижней границы для этих же периодов.
Подстраивайте индикатор RSI
Трейдер, автор и специалист по психологии торговли Александр Элдер упоминает в своей книге “Зарабатываем трейдингом” о подстройке границ RSI таким образом, чтобы индикатор примерно 5% времени находился выше или ниже этих границ. Он предлагает производить подстройку каждые 4-6 месяцев. Вместо эмпирического метода, границы можно определить статистически, для любого количества баров RSI, как было показано выше. Приведенная в данной статье методика расширяет временные рамки индикатора RSI, не ухудшая его способность измерять моментум в акции по нормированной шкале.
Будьте в курсе всех важных событий United Traders — подписывайтесь на наш телеграм-канал
utmagazine.ru
Введение.
Основные понятия:
Диапазон измерения-область значений измеряемой величины, для которой нормированы допустимые погрешности средства измерения.
Верхняя граница диапазона измерения-максимальное значение величины, измеряемое с заданной погрешностью.
Нижняя граница диапазона измерения-минимальное значение величины, измеряемое с заданной погрешностью.
Скорость счета импульсов -количество импульсов, регистрируемых в единицу времени; n-суммарная скорость счета от измерительного фактора и фона; nф-скорость счета от фона.
Чувствительность
средства измерения-отношение
изменения сигнала на выходе к изменению
измеряемой величины. Для блока
детектирования, работающего в импульсном
режиме, чувствительность определяется
как отношение скорости счета к мощности
дозы: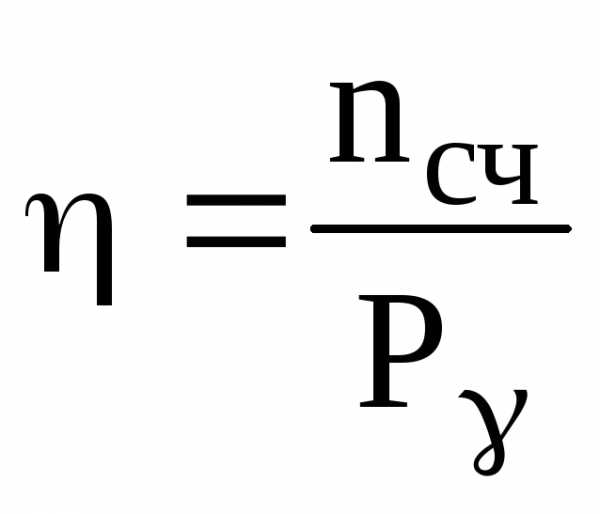 .
.
Распределение-ряд чисел, показывающих, как часто встречаются то или иное значение случайной величины.
Распределение вероятностей-сопоставление множества значений случайной величины их вероятностям.
Случайная величина-переменная величина, принимающая различные значения в зависимости от случайных обстоятельств.
Математическое ожидание (истинное значение измеряемой величины) среднее значение измеряемой величины при бесконечном времени измерений.
Дисперсия-среднее значение квадрата отклонений измеряемой величины от математического ожидания.
Среднее квадратичное (стандартное)отклонение случайной величины-неотрицательное значение корня квадратного из дисперсии.
1.2. Определение нижней границы диапазона измерения блока детектирования.
Измерение мощности
дозы гамма излучения блоками детектирования
с газоразрядными счетчиками, работающими
в импульсном режиме (далее БД) осуществляется
путем измерения количества импульсов
N за некоторое время измерения tизм,
расчета по этим данным скорости счета 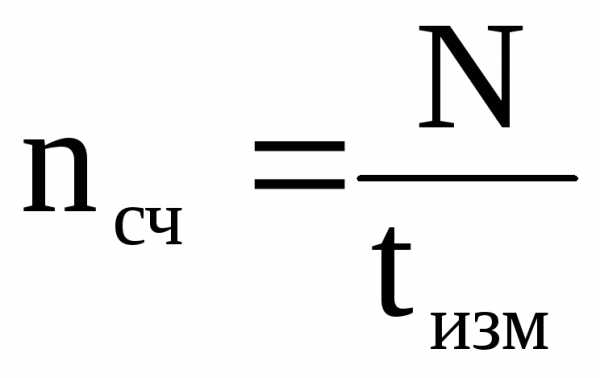 и, затем, мощности дозы:
и, затем, мощности дозы: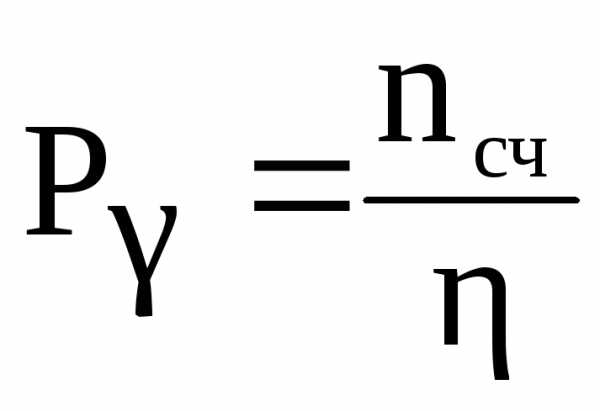 .
.
Верхняя граница диапазона измерения газоразрядным счетчиком определяется погрешностью из-за просчетов, когда регистрируемая частица попадает в счетчик во время, когда он не чувствителен к излучению.
,
здесь tp-разрешающее время прибора.
Нижняя граница диапазона измерения газоразрядным счетчиком определяется погрешностью из-за статистического характера радиоактивного распада, который и является источником гамма излучения.
Дело в том, что поступление импульсов от гамма-излучения неравномерно, как это показано на рис 1.
А)
Б)
Рис.1. Равномерное – А), и неравномерное-Б) – поступление импульсов от БД.
Для того, чтобы точно определить скорость счета импульсов при равномерном (статистическом) их поступлении в принципе необходимо бесконечное время. В этом случае будем иметь истинное значение скорости счета и, следовательно, мощность дозы:.
При конечном времени измерения будем иметь величину в какой-то мере близкую, но все же отличающуюся от истинной.
Разность между измеренной величиной скорости счета и истинной является абсолютной погрешностью измерения .
Отношение величины абсолютной погрешности к истинной скорости счета является относительной погрешностью измерения.
Значение измеренной скорости счета является величиной случайной, зависящей от множества не поддающихся учету факторов. Тем не менее, вероятность получения того или иного значения скорости счета может быть рассчитана с использованием аппарата теории вероятностей.
В соответствии с этой теорией, распределение вероятностей появления того или иного значения числа импульсов N за время измерения tизм подчиняется, при малом уровне активности закону распределения Пуассона.
Согласно этому закону, P(N)-вероятность того, что случайная величина (в нашем случае – количество импульсов) примет определенное значение N, определиться выражением:
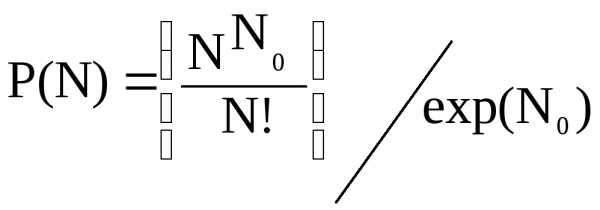
Здесь N0-истинное количество импульсов.
Графически этот закон показан на рис.2.
Р(N)
N0 N
Рис.2. Общий вид распределения вероятностей получения числа импульсов N.
Из графика видно, что наиболее вероятностным является истинное значение –N0 (точнее N0 и N0-1). График тем симметричнее , чем больше N.
Закон Пуассона позволяет определить величину дисперсии результатов измерения:
 (1)
(1)
Величина среднеквадратичного отклонения (абсолютной погрешности):
(2)
Величина среднеквадратичного отклонения (относительной погрешности ):
(3)
Считается, что измеренное значение количества импульсов окажется в области:
N0 с вероятностью 67%
N02 с вероятностью 95%
N03 с вероятностью 99,7%
Из формулы(3) следует, что для измерения количества импульсов за 100 секунд при допустимой погрешности 10% необходимо, чтобы скорость счета была не менее 1 имп/с.
Однако, приведенные соображения справедливы, если на распределение вероятностей влияет только статистический характер измеряемой величины. Реально же погрешность измерения зависит еще и от значения фоновой скорости счета nф, не связанной с измеряемой величиной. Значение nф является случайнойвеличиной, зависящей от свойств счетчика, измерительного прибора и ряда факторов, не поддающихся учету.
Приведенными выше формулами (1)-(3) можно пользоваться лишь при малых значениях величины фона, когда
 ,
или
,
или  (4)
(4)
В противном случае значением фона можно пренебрегать нельзя и тогда величина дисперсии среднего значения имеет вид:
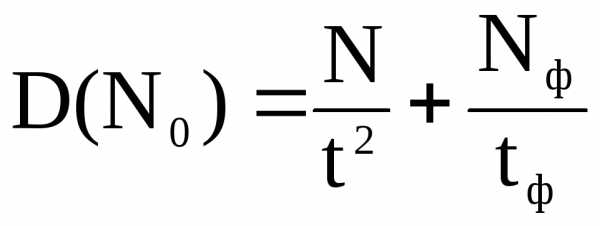 (5)
(5)
Относительная погрешность измерения при этом определяется как корень из суммы квадратов:
(6)
Здесь, как, и выше, величины без индексов обозначают измерение совместно с фоном.
Учет фона усложняет определение нижней границы диапазона измерения. В частности, минимальную, достоверно измеряемую величину мощности дозы (нижнюю границу диапазона измерения) определяется по формулам:
Рmin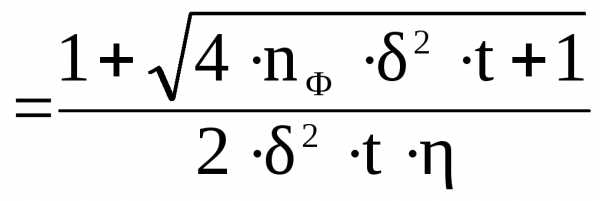 (7)
(7)
Рmin = (8)
Относительную погрешность измерения определяют по формулам:
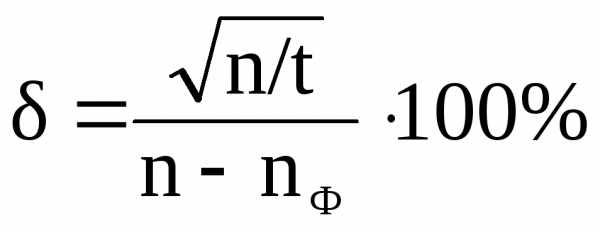 (9)
(9)
(10)
Здесь: t, tФ – время измерения мощности дозы и фона, с;
nф – скорость счета от фона, имп/с;
δ – относительная погрешность, доли;
η – чувствительность блока детектирования, (имп/с) / (Р/час).
Время измерения при заданной статистической погрешности определяют по формулам:
Из формул (7) и (8) следует, что значение нижней границы диапазона измерения тем меньше, чем выше чувствительность блока детектирования, чем больше время измерения и чем ниже уровень фона.
studfiles.net
Точная нижняя граница – Большая Энциклопедия Нефти и Газа, статья, страница 1
Точная нижняя граница
Cтраница 1
Точная нижняя граница а ( К) чисел а, обладающих свойством (1.15), называется константой несплющенности клина К. [1]
Поэтому точная нижняя граница I функции W на сфере е положительна и не может равняться нулю. [2]
Утверждение 3.1. Точная нижняя граница ео множества решений задачи (3.1.11), (3.1.2) – (3.1.10) достигается при отсутствии точек разрыва второго рода и определяется выражением е 3Vo, где V0 ] R / Mv [, Mv – максимально допустимый объем и-го модуля. [3]
Согласно определению точной нижней границы для каждой точки М0, лежащей внутри В, существует такая последовательность fyn ( M) верхних функций, что и ( Ж0) – и ( Ж0) при – оо. Для разных точек Ж0 последовательности tyn ( M) могут быть разными. [4]
Грубо оценить точную нижнюю границу можно следующим образом. Это значение h и является одной из нижних границ оптимальной высоты опт. [6]
Аналогично определяется и точная нижняя граница g числового множества как такое число, которое не превышает ни одного элемента множества и обладает тем свойством, что всякое число, большее чем g, превосходит по крайней мере один элемент множества. Всякое множество, ограниченное снизу, имеет точную нижнюю границу, которая является либо наименьшим элементом множества, либо его нижним пределом. [7]
Но из определения точной нижней границы следует, что при любом е 0 существуют такие точки М из ( Р) п N из ( Q), что ЛШе. [8]
Аналогичные формулы справедливы для точной нижней границы. [9]
Возьмем для каждого / точную нижнюю границу расстояний точек куска ( s -) от точек части ( S) – ( st) поверхности и обозначим через ц наименьшее из этих чисел. Если какая-либо ее точка попадает в некоторое определенное ( s), то вся часть ( У) целиком содержится в соответственном ( st) и, следовательно, вместе с ( s /) обладает требуемым свойством. [10]
Переходя в правой части к точным нижним границам, получим требуемое неравенство. [11]
Решеткой называется упорядоченное множество с точной верхней и точной нижней границей. [12]
В некоторых случаях эта граница является точной нижней границей и существуют оценки параметра, на которых она достигается. Такие оценки являются оптимальными, если качество оценки характеризовать средней квадратической погрешностью, и их называют эффективными. Сравнение дисперсии данной несмещенной оценки с нижней границей дисперсии несмещенных оценок позволяет судить, насколько данная оценка близка к оптимально возможной. [13]
Расстоянием Громова-Хаусдорфа dist ( X, У) называется точная нижняя граница таких чисел А. [14]
Аналогично доказывается, что всякое ограниченное числовое множество имеет точную нижнюю границу g, которая не превосходит нижнего предела a: g ] а. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
